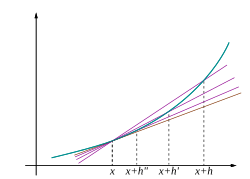下記テーマに関する記事の一部
解析学
基本定理 関数の極限 連続性 平均値の定理
微分法 定義 導関数 (一般化（英語版）) 微分 無限小 関数の 全 概念 微分の記法 二階導関数 三階導関数（英語版） 変数変換（英語版） 陰関数の微分 Related rates（英語版） テイラーの定理 法則と恒等式（英語版） 和（英語版） 積 合成 冪（英語版） 商 一般ライプニッツ ファー・ディ・ブルーノの公式（英語版）
積分法 積分一覧 定義 不定積分 積分 (広義) リーマン積分 ルベーグ積分 線積分 複素線積分 道具 部分 Discs（英語版） 円殻（バウムクーヘン） 置換 三角置換（英語版） 部分分数（英語版） 順序（英語版） 漸化式
級数 幾何 (算術幾何) 調和 交代 冪 二項 テイラー 収束判定法（英語版） 項の極限（項判定法）（英語版） 比 冪根 積分 比較 極限比較（英語版） 交代級数（英語版） 凝集 ディリクレ アーベル（英語版）
ベクトル 勾配 発散 回転 ラプラシアン 方向微分 公式（英語版） 定理 発散 勾配（英語版） グリーン ケルビン・ストークス
多変数 形式と枠組み 行列（英語版） テンソル 外 幾何学的（英語版） 定義 偏微分 多重積分 線積分 面積分 体積分 ヤコビアン ヘッセ行列
特殊化 分数階微積分 解析接続 マリアヴァン（英語版） 確率（英語版） 変分
その他 解析学記号
表 話 編 歴

数学における実変数函数（英語版）の微分係数、微分商または導関数（どうかんすう、英: derivative）は、別の量（独立変数）に依存して決まる、ある量（関数の値あるいは従属変数）の変化の度合いを測るものであり、これらを求めることを微分（びぶん、英: differentiation）するという。微分演算の結果である微分係数や導関数も用語の濫用でしばしば微分と呼ばれる。

微分は解析学分野（特に微分積分学分野）の基本的な道具である。例えば、動く物体の位置の時間に関する導函数はその物体の速度であり、これは時間が進んだときその物体の位置がどれほど早く変わるかを測る。

一変数函数の適当に選んだ入力値における微分係数は、その点におけるグラフの接線の傾きである。これは導函数がその入力値の近くでその函数の最適線型近似を記述するものであることを意味する。そのような理由で、微分係数はしばしば「瞬間の変化率」として記述される。瞬間の変化率は独立変数に依存する従属変数である。

微分は実多変数函数（英語版）にも拡張できる。この一般化において、導函数はそのグラフが（適当な変換の後）もとの函数のグラフを最適線型近似する線型写像と解釈しなおされる。ヤコビ行列はこの線型変換を独立および従属変数を選ぶことで与えられる基底に関して表現する行列であり、独立変数に関する偏微分を用いて計算することができる。多変数実数値函数に対して、ヤコビ行列は勾配に簡約される。

導函数を求める過程を微分あるいは微分法、微分演算（英: differentiation）と言い、その逆の過程（原始函数を求めること）を反微分という。微分積分学の基本定理は反微分が積分と同じであることを主張する。一変数の微分積分学において微分と積分は基本的な操作の二本柱である^[1]。

初めに最も簡単な場合を扱う。すなわち、実数値の変数を1個もち、値も1個の実数であるような関数 f(x)（または単に f とも書く）を微分することを考える。「微分する」というのは、より正確には、微分係数（英語版）または導関数のいずれかを求めることを意味している。

説明を単純にするため、f(x) はすべての実数 x に対して定義されているとしよう。すると各々の実数 a に対して、f の a における微分係数と呼ばれる数がある（定義されない場合もあるが、ここでは理想的な状況のみを想定して説明する）。これを f′(a) で表す。また、実数 a に対して微分係数 f′(a) を対応させる関数 f′ のことを f の導関数という。

微分係数 f′(a) とは何であるか直観的に説明するには、いくつかの方法がある。

1. 微分係数 f′(a) とは、関数 f のグラフに x = a において（すなわち点 (a, f(a)) において）接線をひいたときの、その接線の傾きのことである。
2. 微分係数 f′(a) とは、変数 x の値の変化に伴う f(x) の変化を考えたときの、x = a における f(x) の瞬間変化率のことである。
3. 微分係数 f′(a) とは、関数 f のグラフの x = a 付近を（すなわち点 (a, f(a)) 付近を）限りなく拡大していったときに、グラフが直線に近づいて見える場合における、その直線の傾きのことである。

これらはいずれも、論理的に厳密な定義とはいえない。それは、「接線」や「瞬間変化率」について厳密な定義が与えられていないし、またグラフを「限りなく拡大する」ということの意味も定かではないからである。

ごく単純な関数については、上記の説明が微分係数の具体的な値について十分な示唆を与えるのは確かだ。たとえば一次関数 f(x) = Ax + B を考えると、そのグラフは直線なので、「x = a における接線」もその直線自身であると考えるのが妥当だろう。直線 y = Ax + B の傾きは A だから、微分係数 f′(a) の値も A とすべきだと考えられる。また、二次関数についても、グラフの接線の概念を微分とは無関係に定義して、その傾きを求めることはできる。だが、ほとんどの関数にはこのような手法は通用しないから、一般的な定義を与えるためには新しい考えが必要である。

極限としての変化率

Figure 1. (x, f(x)) における接線

Figure 2. 二点 (x, f(x)) および (x+h, f(x+h)) の定める、曲線 y= f(x) の割線（英語版）

Figure 3. 割線の極限としての接線

Figure 4. 割線の極限としての接線（アニメーション）

関数 f(x) が開区間 ${\displaystyle I\subset \mathbb {R} }$ において定義されているとする。そのとき、${\displaystyle a\in I}$ に対し、極限

${\displaystyle \lim _{h\to 0}{\frac {f(a+h)-f(a)}{h))}$

が存在するとき、f(x) は x = a において微分可能であるという（極限は有限確定値であることを要請する。すなわち、正の無限大や負の無限大であることは許容しない）。またそのとき、上記の極限を x = a における f(x) の微分係数とよび、f′(a) によって表す。

これにともない、f(x) のグラフ上の点 (a, f(a)) を通り傾き f′(a) をもつ直線のことを、f(x) のグラフの x = a における接線という。つまり、x = a における接線とは、y = f′(a)(x − a) + f(a) によって与えられる直線のことである。

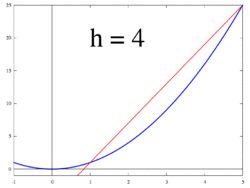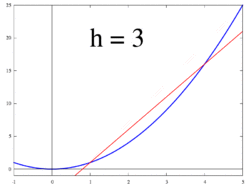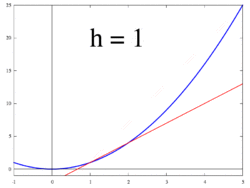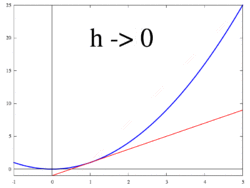
上述の微分係数の定義に現れる分数

${\displaystyle {\frac {f(a+h)-f(a)}{h))}$

は差分商とよばれる。これは関数 f(x) のグラフ上の2点 (a, f(a)) と (a + h, f(a + h)) を通る直線（割線という）の傾きを表している。あるいは、変数 x の値が a から a + h まで変化するあいだの、関数の値の平均変化率を表しているとみることもできる。これらの見方によれば、微分係数の定義について、次のような解釈を与えることができる。

1. グラフ上の2点 (a, f(a)), (a + h, f(a + h)) を通る割線が、h を 0 へと近づけたときにある直線に近づくならば、それを接線とみなすのが妥当であろう。この意味での接線の傾きが、微分係数 f′(a) である。
2. 「変数 x の値が a から a + h まで変化するあいだの関数値の平均変化率」が、h を 0 へと近づけたときにある数に近づくならば、それを瞬間変化率とみなすのが妥当であろう。この瞬間変化率が、微分係数 f′(a) である。

なお、上述の微分可能性の定義では h が 0 にどのようにして近づいても差分商が一定の値に収束することを要請したが、近づき方を限定することも考えられる。h が正の値をとりながら 0 に近づいたときの片側極限

${\displaystyle \lim _{h\searrow 0}{\frac {f(a+h)-f(a)}{h))}$

が存在するとき、f(x) は x = a において右側微分可能であるといい、この片側極限を右側微分係数とよぶ。同様に、h が負の値をとりながら 0 に近づいたときの片側極限

${\displaystyle \lim _{h\nearrow 0}{\frac {f(a+h)-f(a)}{h))}$

が存在するとき、f(x) は x = a において左側微分可能であるといい、この片側極限を左側微分係数とよぶ。f(x) が x = a において微分可能であるためには、「f(x) が x = a において右側微分可能かつ左側微分可能で、かつ右側微分係数と左側微分係数が一致する」ということが必要十分である。

関数 f(x) が開区間 ${\displaystyle I\subset \mathbb {R} }$ で定義されており、すべての ${\displaystyle a\in I}$ において微分可能であるとき、f は区間 I において微分可能であるという。またそのとき、a に対して微分係数 f(a) を対応させる区間 I 上の関数のことを、f の導関数といい f′（または変数の記号を補って f′(x)）で表す。

I がその他のタイプの区間である場合にも、区間 I における微分可能性を定義することができる。たとえば、I が有界閉区間 [α, β] である場合には、区間の内点では通常の意味での微分係数の存在を要請し、α では右側微分係数が、β では左側微分係数が存在することを要請する。導関数 f′(x) の値は、x = α では右側微分係数、x = β では左側微分係数とする。

関数 f が区間 I において微分可能で、さらに導関数 f′ が I で連続であるとき、f は I において連続微分可能である、または C¹ 級であるという。

開区間 ${\displaystyle I\subset \mathbb {R} }$ で定義された関数 f(x) について、${\displaystyle a\in I}$ とするとき、次の条件は f(x) の x = a における微分可能性と同値である。

ある定数 A が存在して、h → 0 のとき f(a + h) = f(a) + Ah + o(h) である。

ここで o(h) はランダウの記号である。この条件が成り立つとき、A は微分係数 f′(a) に他ならない。

「h → 0 のとき f(a + h) = f(a) + Ah + o(h)」が成り立つことを指して、f(a) + Ah は f(a + h) の x = a における1次近似であるという。この言葉を用いれば、一点における微分可能性とは1次近似可能性のことだといえる。またこれは、#直観的な説明の、微分係数に関する3番目の説明を厳密化したものとみることができる。

関数 f(x) が x = a において微分可能ならば、 f(x) は x = a で必ず連続である。

一方で、関数がある一点で連続だったとしても、そこで微分可能でないことがある。

• 絶対値関数 f(x) = |x| は x = 0 において連続だが、この点で微分可能でない。h > 0 のときは (0, 0), (h, f(h)) を通る割線の傾きは 1 だが、h < 0 のときは −1 である。この例では、グラフは x = 0 においてカスプ（尖点）をもつという言い方をする。
• 関数 f(x) = x^1/3 は x = 0 において連続だが、この点で微分可能でない。(0, 0), (h, f(h)) を通る割線の傾きは、h → 0 のとき正の無限大に発散するからである。この例は、グラフが滑らかにつながっているからといって微分可能とはかぎらないことを示している。

実用上現れる関数の大半は、ほとんど至るところで微分可能である。微分積分学の歴史（英語版）の初期には、多くの数学者は連続関数はほとんど至るところで微分可能であると考えていた。この仮定は緩やかな条件、たとえば単調写像やリプシッツ連続などのもとでは確かに満たされる。しかし1872年にワイエルシュトラスは、至るところ連続だが、至るところ微分不可能な関数の例を与えた（ワイエルシュトラス関数）。1931年にステファン・バナフは、連続関数全体のなす空間において、少なくとも1点で微分可能な関数全体のなす集合が痩せている(meager)ことを示した^[2]。くだけた言い方をすれば、ほとんどあらゆる連続関数がすべての点で微分不可能なのである。

関数 f が区間 I で導関数 f ′ をもち、それがさらに I で微分可能なとき、f ′ の導関数を f の2階導関数とよび f ″ で表す。より一般に、関数 f が区間 I で n 回繰り返して微分できるとき、f は I で n 回微分可能であるといい、n 回微分して得られる関数を n 階導関数といって f ⁽ⁿ⁾ で表す。

f が n 回微分可能であって、さらに n 階導関数 f ⁽ⁿ⁾ が連続であるとき、f は n 回連続微分可能である（または C ⁿ 級である）という。何回でも微分可能な関数は無限回微分可能である（または C ^∞ 級である）という。C ^∞ 級関数のことを滑らかな関数ということもある（ただしこの語の用法は必ずしも一定していず、たとえば単に微分可能であることを指して滑らかであるという場合もある）。

微分可能な関数 f(x) について、導関数 f′(x) が正の値をとる区間では、f(x) の値は単調増加する（より詳しくいえば、狭義単調増加する）。導関数 f′(x) が負の値をとる区間では f(x) の値は単調減少する。導関数 f′(x) の値がつねに 0 であるような区間では、関数 f(x) の値は一定である。

2階微分可能な関数 f(x) について、2階導関数 f′′(x) が正の値をとる区間では、関数 f(x) は凸（下に凸）である。f′′(x) が負の値をとる区間では関数 f(x) は凹（上に凸）である。

関数 f(x) が x = a の前後で凸から凹に、あるいは凹から凸に切り替わるとき、点 (a, f(a)) は f(x) のグラフの変曲点であるという^[3]。2階微分可能な関数 f(x) については、これは2階導関数 f′′(x) の符号が切り替わる x の値に対応する点ということができる。

関数 f が開区間 I で n − 1 階微分可能で、n − 1 階導関数 f^{(n − 1)} が x = a で微分可能なとき、f^{(n − 1)} の x = a における微分係数を f⁽ⁿ⁾(a) とすれば

${\displaystyle f(a+h)={\frac {f(a)}{0!))+{\frac {f'(a)h}{1!))+{\frac {f''(a)}{2!))h^{2}+\dots +{\frac {f^{(n)}(a)}{n!))h^{n}+O(h^{n})}$

が成り立つ（テイラーの定理のペアノの剰余項による形）。これは、前述の、一点における微分可能性の1次近似による定式化の一般化にあたる。

実数値の変数 x をもち、${\displaystyle \mathbb {R} ^{m))$ に値をもつベクトル値函数 f(x) = (f₁(x), …, f_m(x)) を考える。これが一点 x = a において微分可能であるというのは、

${\displaystyle \lim _{h\to 0}{\frac {f(a+h)-f(a)}{h))}$

という極限が存在することである^{[注釈 1]}。上記の極限として現れるベクトルを f′(a) で表す（これも${\displaystyle \mathbb {R} ^{m))$の元である）。一般には f′(a) に特に名前はないが、f(x) が ${\displaystyle \mathbb {R} ^{m))$ における点の位置の変化（曲線といってもよい）を表しているとみなす場合は、f′(a) を速度とよぶことがある。

f(x) = (f₁(x), …, f_m(x)) が x = a において微分可能であることと、各成分 f_i(x) がすべて x = a において微分可能であることは同値である。また

${\displaystyle f'(a)=(f'_{1}(a),\dots ,f'_{m}(a))}$

が成り立つ。

ベクトル値関数 f(x) が区間 I の各点で微分可能なとき、f(x) は区間 I において微分可能であるという。

ベクトル値関数については、高階微分も同様にして考えることができる。f′′(a) は、f(x) が ${\displaystyle \mathbb {R} ^{m))$ における点の位置の変化を表しているとみなす場合は、加速度とよばれる。

実数を拡大して超実数 R^* (⊃ R) の体系の中で考えるとき、実函数 y = f(x) の実点 x における微分係数は（f の超実数への自然延長をやはり f と書くとき）、無限小 ∆x に対して ∆y = f(x+ ∆x) - f(x) とすれば、Δy の Δx に関する商 ∆y/∆x の標準部（英語版） を考えることで定義することができる。ここで、上記の差分商の標準部が無限小 ∆x の取り方に依らずに定まるとき、すなわち

${\displaystyle \exists !m\in \mathbb {R} ,\forall {\mathit {\Delta x))({\mathit {\Delta x))\in \operatorname {monad} (0)\land {\mathit {\Delta x))\neq 0),\;m=\operatorname {st} \!\left({\frac {f(a+{\mathit {\Delta x)))-f(a)}{\mathit {\Delta x))}\right)}$

が成り立つとき、この実数 m を実函数 f の a における微分係数と呼ぶ。

関数 f(x) の導関数や高階導関数を表す記法には次のようなものがある^[4]。

また、y = f(x) とおいて、下記の記法における f を y で置き換えた記法も用いられる。

導関数や高階導関数を表す記法

	導関数	2階導関数	3階導関数	n 階導関数
ラグランジュの記法	f′	f″	f′′′	f(n)
ライプニッツの記法	${\displaystyle {\frac {df}{dx))}$	${\displaystyle {\frac {d^{2}f}{dx^{2))))$ または ${\displaystyle {\frac {d^{2)){dx^{2))}f}$	${\displaystyle {\frac {d^{3}f}{dx^{3))))$ または ${\displaystyle {\frac {d^{3)){dx^{3))}f}$	${\displaystyle {\frac {d^{n}f}{dx^{n))))$ または ${\displaystyle {\frac {d^{n)){dx^{n))}f}$
ニュートンの記法	${\displaystyle {\dot {f))}$	${\displaystyle {\ddot {f))}$	${\displaystyle {\overset {...}{f))}$	（通常使われない）
ルイ・アーボガスト（英語版）の記法[注釈 2]	Df または Dxf	D2f または ${\displaystyle D_{x}^{2}f}$	D3f または ${\displaystyle D_{x}^{3}f}$	Dnf または ${\displaystyle D_{x}^{n}f}$

点 a における微分係数（および高階の微分係数）を表すには、(a) を添えたり | _{x = a} を添えたりする。

例えば、

${\displaystyle f^{(n)}(a)={\frac {d^{n}f}{dx^{n))}(a)=\left.{\frac {d^{n}f}{dx^{n))}\right|_{x=a}=D^{n}f(a)=\left.D^{n}f\right|_{x=a}=\left.y^{(n)}\right|_{x=a}=\left.{\frac {d^{n}y}{dx^{n))}\right|_{x=a))$

である。

u, v が微分可能な x の函数で、a, b が x に無関係な定数のとき

• 線型性:

  ${\displaystyle (au+bv)'=au'+bv'.}$

• 積の微分法則:

  ${\displaystyle (uv)'=u'v+uv',}$

  ${\displaystyle {\begin{aligned}{\frac {d(u_{1}u_{2}\cdots u_{n})}{\mathit {dx))}&=\sum _{i=1}^{n}u_{1}\cdots u_{i-1}{\frac {du_{i)){\mathit {dx))}u_{i+1}\cdots u_{n}\\&={\frac {du_{1)){\mathit {dx))}u_{2}u_{3}\cdots u_{n}+u_{1}{\frac {du_{2)){\mathit {dx))}u_{3}\cdots u_{n}+\cdots +u_{1}u_{2}\cdots u_{n-1}{\frac {du_{n)){\mathit {dx))},\end{aligned))}$

  ${\displaystyle {\frac {d^{n}(uv)}((\mathit {dx))^{n))}=\sum _{i=0}^{n}{n \choose i}u^{(n-i)}v^{(i)}.}$

• 連鎖律 (Chain-rule):

  ${\displaystyle {\frac {d(u\circ v)}{\mathit {dx))}={\frac {du}{\mathit {dv))}\cdot {\frac {dv}{\mathit {dx))}.}$

いくつかの初等関数に関して、特徴的な微分公式が挙げられる。e^x、a^x、log_e x、log_ax はそれぞれ指数関数と対数であり、sin、cos、tan は三角関数、arcsin、arccos、arctan は三角函数の逆函数（逆三角関数）、sinh、cosh、tanh は双曲線関数、arsinh、arcosh、artanh は双曲線函数の逆函数（逆双曲線関数）である。また、三角函数および双曲線函数の冪乗は cos²x ≔ (cos x)² のように函数名の肩に指数を書いて表していることに注意。

初等関数の微分

原始関数	導関数	備考
${\displaystyle \mathrm {e} ^{x))$	${\displaystyle \mathrm {e} ^{x))$	指数関数の微分
${\displaystyle a^{x))$	${\displaystyle \left(\log _{e}a\right)a^{x))$	一般の底の指数函数に対する微分
${\displaystyle \log _{e}x}$	${\displaystyle {1 \over x))$	自然対数の微分
${\displaystyle \log _{a}x}$	${\displaystyle {1 \over x\log _{e}a))$	一般の底の対数に対する微分
${\displaystyle x^{a))$	${\displaystyle ax^{a-1))$	冪乗の微分
${\displaystyle \sin x}$	${\displaystyle \cos x}$	正弦函数の微分
${\displaystyle \cos x}$	${\displaystyle -\sin x}$	余弦函数の微分
${\displaystyle \tan x}$	${\displaystyle {1 \over \cos ^{2}x}=1+\tan ^{2}x}$	正接函数の微分
${\displaystyle \arcsin x}$	${\displaystyle {1 \over {\sqrt {1-x^{2)))),\quad \left(-1<x<1\right)}$	逆正弦函数の微分
${\displaystyle \arccos x}$	${\displaystyle -{1 \over {\sqrt {1-x^{2)))),\quad \left(-1<x<1\right)}$	逆余弦函数の微分
${\displaystyle \arctan x}$	${\displaystyle {1 \over 1+x^{2))}$	逆正接函数の微分
${\displaystyle \sinh x}$	${\displaystyle \cosh x}$	双曲線正弦函数の微分
${\displaystyle \cosh x}$	${\displaystyle \sinh x}$	双曲線余弦函数の微分
${\displaystyle \tanh x}$	${\displaystyle {1 \over \cosh ^{2}x}=1-\tanh ^{2}x}$	双曲線正接函数の微分
${\displaystyle \operatorname {arsinh} x}$	${\displaystyle {1 \over {\sqrt {1+x^{2))))}$	逆双曲線正弦函数の微分
${\displaystyle \operatorname {arcosh} x}$	${\displaystyle {1 \over {\sqrt {x^{2}-1))},\quad \left(|x|>1\right)}$	逆双曲線余弦函数の微分
${\displaystyle \operatorname {artanh} x}$	${\displaystyle {1 \over {1-x^{2))},\quad \left(-1<x<1\right)}$	逆双曲線正接函数の微分

n 個の実数値変数をもつ多変数関数 f(x₁, …, x_n) が与えられたとする（f はスカラー値でなくベクトル値でもよい）。各 x_j について、x_j を除く n − 1 個の変数の値を固定することにより、f(x₁, …, x_n) を変数 x_j のみをもつ1変数関数とみなすことができる。そのようにみた上で f(x₁, …, x_n) を変数 x_j について微分するのが偏微分とよばれる操作である。

f(x₁, …, x_n) が ${\displaystyle \mathbb {R} ^{n))$ の開集合 D で定義されているとする。点 ${\displaystyle (a_{1},\dots ,a_{n})\in D}$ に対し、x_j 以外の変数を x_k = a_k とおいて固定し、

${\displaystyle f(a_{1},\dots ,a_{j-1},x_{j},a_{j+1},\dots ,a_{n})}$

という x_j の1変数関数を考える。その x_j = a_j における微分係数

${\displaystyle \lim _{h\to 0}{\frac {f(a_{1},\ldots ,a_{j-1},a_{j}+h,a_{j+1},\ldots ,a_{n})-f(a_{1},\ldots ,a_{j-1},a_{j},a_{j+1},\ldots ,a_{n})}{h))}$

を、f(x₁, …, x_n) の点 (a₁, …, a_n) における x_j に関する偏微分係数といい、

${\displaystyle f_{x_{j))(a_{1},\ldots ,a_{n})}$, ${\displaystyle {\frac {\partial f}{\partial x_{j))}(a_{1},\ldots ,a_{n})}$, ${\displaystyle \partial _{x_{j))f(a_{1},\ldots ,a_{n})}$

などの記号で表す。また、点 (a₁, …, a_n) に対してこれらの偏微分係数を対応づける D 上の関数を f(x₁, …, x_n) の x_j に関する偏導関数といい、

${\displaystyle f_{x_{j))}$, ${\displaystyle {\frac {\partial f}{\partial x_{j))))$, ${\displaystyle \partial _{x_{j))f}$

などで表す。丸い d の記号 ∂ は偏微分記号などとよばれる。

f(x₁, …, x_n) が D の各点ですべての変数について偏微分可能で、かつすべての偏導関数 ∂f/∂x_j が D で連続であるとき、関数 f は D で連続微分可能（または C¹ 級）であるという。

偏微分を繰り返して行うことにより得られる微分係数のことを高階の偏微分係数という。これは微分の階数について帰納的に定義される。

たとえば f(x₁, …, x_n) の点 a = (a₁, …, a_n) における2階偏微分係数

${\displaystyle {\frac {\partial ^{2}f}{\partial x_{j_{1))\partial x_{j_{2))))(a)}$

は次のように定義される。前提として、導関数 ∂f/∂x_j2 が存在するものとする。この仮定のもとで、 ∂f/∂x_j2 が点 a において x_j1 に関して偏微分可能ならば、その偏微分係数のことを上記の記号で表すのである。∂f/∂x_j2 があらゆる点 a において x_j1 に関して偏微分可能であるとき、点 a に上記の2階偏微分係数を対応づける関数のことを、

${\displaystyle {\frac {\partial ^{2}f}{\partial x_{j_{1))\partial x_{j_{2))))}$

と書いて2階偏導関数とよぶ。同様のことを繰り返して、一般の k 階偏微分係数

${\displaystyle {\frac {\partial ^{k}f}{\partial x_{j_{1))\partial x_{j_{2))\dotsb \partial x_{j_{k))))(a)}$

および k 階偏導関数

${\displaystyle {\frac {\partial ^{k}f}{\partial x_{j_{1))\partial x_{j_{2))\dotsb \partial x_{j_{k))))}$

が定義される。

微分の順序交換については次が知られている。2変数関数 f(x, y) について、2階偏導関数 ∂²f/∂x∂y, ∂²f/∂y∂x がともに存在して、さらにいずれも点 a において連続ならば、

${\displaystyle {\frac {\partial ^{2}f}{\partial x\,\partial y))(a)={\frac {\partial ^{2}f}{\partial y\,\partial x))(a)}$

が成立する。2階偏導関数の連続性の仮定が満たされなければこの等式は一般には成立しない。n 変数関数の微分の順序交換についても同じことがいえる。

関数 f(x₁, …, x_n) について、偏微分は f の各座標軸方向への変化を測る。f の任意の方向への変化を測るのが方向微分である。

ベクトル v = (v₁, …, v_n) に対して、関数 f の点 a = (a₁, …, a_n) における v 方向への方向微分係数とは、

${\displaystyle \lim _{h\to 0}{\frac {f(a+hv)-f(a)}{h))}$

のことである。x_j 軸正の方向の単位ベクトルを e_j とするとき、e_j 方向への方向微分係数は、x_j に関する偏微分係数に他ならない。

f が点 a においてすべての変数に関して偏微分可能ならば、あらゆるベクトル v について、点 a における v 方向への方向微分係数が存在する。またこのとき、方向微分係数は v に関して線型である。特に、v = (v₁, …, v_n) に対して方向微分係数 D_vf(a) は

${\displaystyle D_{v}f(a)=\sum _{j=1}^{n}v_{j}{\frac {\partial f}{\partial x_{j))}(a)}$

によって与えられる。

f が Rⁿ の開集合から R^m への函数ならば、f の方向微分は、その点における f の選択した方向への最適線型近似を与える。しかし、 n > 1 のときは、位置方向への方向微分だけでは f の挙動を完全に捉えることはできない。全微分は、全ての方向を一度にまとめて考えることで函数の挙動を完全にとらえるものである。

f の a における全微分係数（あるいは単に全微分）は

${\displaystyle \lim _{\mathbf {h} \to 0}{\frac {\lVert f(\mathbf {a} +\mathbf {h} )-f(\mathbf {a} )-f'(\mathbf {a} )\mathbf {h} \rVert }{\lVert \mathbf {h} \rVert ))=0}$

を満たす唯一の線型写像 f ′(a): Rⁿ → R^m と定義される。ただし、h ∈ Rⁿ だから分母におけるノルムは Rⁿ における標準ノルムであり、他方 f ′(a)h ∈ R^m であり分子のノルムは R^m の標準ノルムである。v が a を始点とするベクトルならば、f ′(a)v は f による v の押し出しと呼ばれ、f_∗v とも書かれる。f の点 a における全微分係数 f ′(a) は a を始点とする任意のベクトル v に対して、線型近似公式

${\displaystyle f(\mathbf {a} +\mathbf {v} )\approx f(\mathbf {a} )+f'(\mathbf {a} )\mathbf {v} }$

が満足される。一変数の微分係数のときと同じく f ′(a) はこの近似の誤差が可能な限り最小となるように選ばれる。高次元の場合に、この線型近似公式が意味を持つためには f ′(a) は Rⁿ のベクトルを R^m のベクトルへ写す線型写像でければならず、また f ′(a)v はその写像の v における値でなければならない。

点 a において全微分係数が存在するならば、a における f の任意の偏微分および方向微分が存在する。即ち、任意の v に対して f ′(a)v が f の a における v-方向への方向微分になる。f を座標成分函数を用いて f = (f₁, f₂, …, f_m) と書けば、全微分係数は、偏微分を用いて行列として表すことができる。この行列

${\displaystyle f'(\mathbf {a} )=\operatorname {Jac} _{\mathbf {a} }=\left({\frac {\partial f_{i)){\partial x_{j))}\right)_{ij))$

は f の a におけるヤコビ行列と呼ばれる。全微分係数 f ′(a) が存在することは、すべての偏微分が存在することよりも真に強い条件であるが、偏微分が全て存在して連続ならば全微分は存在し、それはヤコビ行列によって与えられ、a に関して連続的に変化する。

全微分係数の定義は一変数の場合も含むものになっている。f が実一変数の実数値函数であるとき、全微分係数の存在する必要十分条件は通常の微分係数が存在することである。ヤコビ行列は微分係数 f ′(x) を唯一の成分とする 1 × 1 行列であり、この行列は f(a + h) ≈ f(a) + f ′(a)h なる近似性質を持つ。変数を取り替える（英語版）違いを除いて、これは函数 x ↦ f(a) + f ′(a)(x − a) が f の a における最適線型近似であることを述べるものである。

函数の全微分をとる操作では、一変数の場合と同じやり方で考えたのでは、別の函数（導函数）を与えることは無い。これは多変数函数の全微分係数が一変数函数の微分係数よりも多くの情報をもつものであることからくるもので、実際に全微分は函数の始域となる空間の接束から終域となる空間の接束への写像を与えるものになっている。

自然な意味で高階導函数に対応する概念は、線型写像でも接束上の写像でもなく、また全微分を繰り返すことで構成されるものでもない。

ジェット

高階の全導函数となるべきものはジェット（英語版）と呼ばれるもので、これは線型写像ではない（高階導函数は凹性（凸性）などの微妙な幾何学的性質を反映するので、これはベクトルのような線型の情報では記述できない）し、接束上の写像でもない（接束は底空間と方向微分に対してしか意味を成さない）。ジェットは高階の情報を反映することから、各方向への高階の変化を表す追加の座標を引数としてとる。このような余分の座標によって決定される空間はジェット束（英語版）と呼ばれる。函数の全微分と偏微分との関係に並列に対応するものは、函数の k-階のジェットと k 階以下の偏微分との関係として理解することができる。

高階フレシェ微分

全微分を繰り返しとることは、高階のフレシェ微分（を R^p に特殊化したもの）として定式化することができる。つまり、k-階の全微分は

${\displaystyle D^{k}f\colon \mathbb {R} ^{n}\to L^{k}(\mathbb {R} ^{n}\times \cdots \times \mathbb {R} ^{n},\,\mathbb {R} ^{m})}$

なる写像として解釈することができる。この写像は点 x ∈ Rⁿ に対して、Rⁿ から R^m への k-多重線型写像の空間の元で、その点において f を（ある特定の明確な意味において）「最適」に k-重線型近似するものを割り当てる。対角線埋め込み Δ: x → (x, x, …, x) との合成を考えれば、多変数のテイラー級数も最初の方の項が

${\displaystyle {\begin{aligned}f(\mathbf {x} )&\approx f(\mathbf {a} )+(Df)(\mathbf {x} )+(D^{2}f)(\Delta (\mathbf {x-a} ))+\cdots \\&=f(\mathbf {a} )+(Df)(\mathbf {x-a} )+(D^{2}f)(\mathbf {x-a} ,\mathbf {x-a} )+\cdots \\&=f(\mathbf {a} )+\sum _{i}(Df)_{i}(\mathbf {x-a} )^{i}+\sum _{j,k}(D^{2}f)_{jk}(\mathbf {x-a} )^{j}(\mathbf {x-a} )^{k}+\cdots \end{aligned))}$

となるようなものとして与えられる。ただし、f(a) は定値函数と同一視され、各 (x − a)ⁱ はベクトル x − a の第 i-成分で、(Df)_i, (D²f)_jk, … は線型変換としての Df, D²f, … の各成分を表す。

微分の概念を多くの他の状況設定の下でも拡張して定義することができる。共通することは、一つの点における函数の導函数がその点における函数の線型近似として働くことである。

• 実函数の微分の重要な一般化は、複素平面上の領域からガウス平面 C への函数のような複素数の複素解析である。複素函数の微分の概念は、実函数の微分の定義において実変数であるところを複素変数に置き換えることで得られる。二つの実数 x, y を用いて複素数 z = x + i y と書くことによりガウス平面 C を座標平面 R² と同一視するとき、C から C への複素可微分函数は R² から R² へのある種の（その偏導函数が全て存在するという意味での）実可微分函数とみなすことができるが、逆は一般には成り立たない（複素微分が存在するのは実導函数が「複素線型」であるときに限り、これは二つの偏導函数がコーシー–リーマンの方程式と呼ばれる関係式を満足することを課すものである）。正則関数の項を参照。
• 別の一般化として可微分多様体（滑らかな多様体）の間の写像の微分を考えることができる。直観的に言えば、可微分多様体 M とはその各点 x の近くで接ベクトル空間と呼ばれるベクトル空間によって近似することのできる空間である（原型的な例は R³ 内の滑らかな曲面（英語版）である）。そのような多様体間の可微分写像 f: M → N の点 x ∈ M における微分係数あるいは微分は、x における M の接空間から f(x) における N の接空間への線型写像であり、導函数は M の接束から N の接束への写像となる。この定義は微分幾何学において基本的であり、多くの応用がある。写像の微分（押し出し）および引き戻し (微分幾何学)（英語版）の項を参照。
• バナッハ空間やフレシェ空間のような無限次元線型空間の間の写像に対する微分法も定義できる。方向微分の一般化であるガトー微分や関数の微分の一般化であるフレシェ微分などがある。
• 古典的な微分の欠点は微分可能な函数がそれほどまでには多くないことである。それにも関わらず、微分の概念を拡張して任意の連続函数やほかの多くの函数を微分可能とするものに、弱微分がある。これは連続函数をより大きな分布の空間に埋め込んで、「平均の上で」のみ微分可能性を課すというものである。
• 微分の性質に着想を得て代数学や位相空間論における同様の対象がたくさん導入され研究されている。例えば導分（英語版）、微分環などを参照。
• 微分の離散的対応物は有限差分である。微分法の研究は時間尺度微分積分学において差分法と統一される。
• 算術微分（英語版）（数論的微分）

プロジェクト 数学

ポータル 数学

• 微分可能関数

• スケール因子 - 異なる物理量間で微分を考える際、得られる値は実際の比というより、物理単位の取り方に依存した仮想的な値になる。

• Crowell, Benjamin (2003), Calculus, http://www.lightandmatter.com/calc/ 
• (Govt. of TN), TamilNadu Textbook Corporation (2006), Mathematics- vol.2, http://www.textbooksonline.tn.nic.in/Books/11/Std11-Maths-EM-2.pdf 
• Garrett, Paul (2004), Notes on First-Year Calculus, University of Minnesota, http://www.math.umn.edu/~garrett/calculus/ 
• Hussain, Faraz (2006), Understanding Calculus, http://www.understandingcalculus.com/ 
• Keisler, H. Jerome (2000), Elementary Calculus: An Approach Using Infinitesimals, http://www.math.wisc.edu/~keisler/calc.html 
• Mauch, Sean (2004), Unabridged Version of Sean's Applied Math Book, オリジナルの2006年4月15日時点におけるアーカイブ。, https://web.archive.org/web/20060415161115/http://www.its.caltech.edu/~sean/book/unabridged.html 
• Sloughter, Dan (2000), Difference Equations to Differential Equations, http://synechism.org/drupal/de2de/ 
• Strang, Gilbert (1991), Calculus, http://ocw.mit.edu/ans7870/resources/Strang/strangtext.htm 
• Stroyan, Keith D. (1997), A Brief Introduction to Infinitesimal Calculus, http://homepage.math.uiowa.edu/~stroyan/Site/Infinitesimals.html 

ウィキブックスに微分関連の解説書・教科書があります。

• Hazewinkel, Michiel, ed. (2001), “Derivative”, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Derivative 
• Khan Academy: "Newton, Leibniz, and Usain Bolt"
• Weisstein, Eric W. "Derivative". mathworld.wolfram.com (英語).
• Online Derivative Calculator from Wolfram Alpha.
• Derivatives of Trigonometric functions, UBC