Punto de inflexión
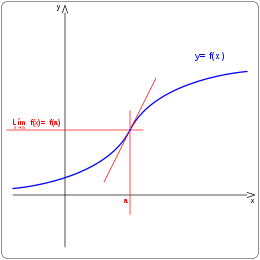
En la matemática, un punto de inflexión de una función, es un punto donde los valores de una función continua en x pasan de un tipo de concavidad a otra. La curva «atraviesa» la tangente.[1] Matemáticamente, la segunda derivada de la función f en el punto de inflexión es cero,[2][3] o no existe.[4]
En el cálculo de varias variables a estos puntos de inflexión se les conoce como puntos de ensilladura.
Cálculo de los puntos de inflexión en funciones reales derivables de variable real
En las funciones derivables reales de una variable real, para hallar estos puntos de inflexión, basta con igualar la segunda derivada de la función a cero y despejar los puntos de x que cumplen esta condición. Los puntos obtenidos deberán ser sustituidos en la derivada tercera o sucesivas hasta que nos dé un valor diferente de cero.[5] Cuando esto suceda, si la derivada para la que es distinto de cero es impar, se trata de un punto de inflexión; pero, si se trata de derivada par, no lo es.[6][7] Más concretamente:
- Se halla la primera derivada de
- Se halla la segunda derivada de
- Se halla la tercera derivada de
- Se iguala la segunda derivada a 0:
- Se despeja la variable independiente y se obtienen todos los valores posibles de la misma: .
- Se halla la imagen de cada sustituyendo la variable dependiente en la función.
- Ahora, en la tercera derivada, se sustituye cada :
- Si , se tiene un punto de inflexión en .
- Si , debemos sustituir en las sucesivas derivadas hasta sea distinto de cero. Cuando se halle la derivada para la que no sea nulo, hay que ver qué derivada es:
- Si la derivada es impar, se trata de un punto de inflexión.
- Si la derivada es par, no se trata de un punto de inflexión.
La ecuación no tiene puntos de inflexión, porque la derivada segunda es siempre mayor o igual a cero, por tanto no hay cambio de concavidad dado que es no negativa en todo su dominio. Sin embargo en la derivada segunda se anula y la primera derivada no nula en es la derivada cuarta, que es par. Obsérvese que tampoco presenta un extremo en .
Galería de ejemplos
Derivada igual a cero

- Función continua y derivable en a
- f'(a)= 0
- Función creciente para x < a.
- Función decreciente para x > a.
- Función estacionaria en a.

- Función continua y derivable en a
- f'(a)= 0
- Función decreciente para x < a.
- Función creciente para x > a.
- Función estacionaria en a.
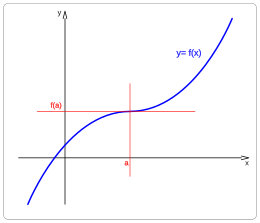
- Función continua y derivable en a
- f'(a)= 0
- Función creciente para x < a.
- Función creciente para x > a.
- Función estacionaria en a.

- Función continua y derivable en a
- f'(a)= 0
- Función decreciente para x < a.
- Función decreciente para x > a.
- Función estacionaria en a.
Derivada mayor que cero
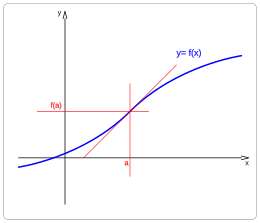
- Función continua y derivable en a
- f'(a)> 0
- Función creciente para x < a.
- Función creciente para x > a.
- Función creciente en a.
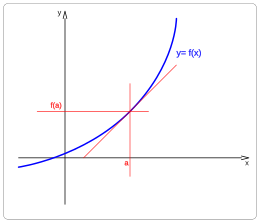
- Función continua y derivable en a
- f'(a)> 0
- Función creciente para x < a.
- Función creciente para x > a.
- Función creciente en a.

- Función continua y derivable en a
- f'(a)> 0
- Función creciente para x < a.
- Función creciente para x > a.
- Función creciente en a.

- Función continua y derivable en a
- f'(a)> 0
- Función creciente para x < a.
- Función creciente para x > a.
- Función creciente en a.
Derivada menor que cero

- Función continua y derivable en a
- f'(a)< 0
- Función decreciente para x < a.
- Función decreciente para x > a.
- Función decreciente en a.

- Función continua y derivable en a
- f'(a)< 0
- Función decreciente para x < a.
- Función decreciente para x > a.
- Función decreciente en a.

- Función continua y derivable en a
- f'(a)< 0
- Función decreciente para x < a.
- Función decreciente para x > a.
- Función decreciente en a.

- Función continua y derivable en a
- f'(a)< 0
- Función decreciente para x < a.
- Función decreciente para x > a.
- Función decreciente en a.
Derivada infinita
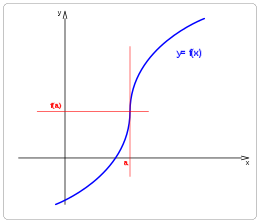
- Función continua y derivable en a
- Función creciente para x < a.
- Función creciente para x > a.
- Función creciente en a.
- Para x < a la función es convexa.
- Para x > a la función es cóncava.
- Para x = a punto de inflexión vertical.
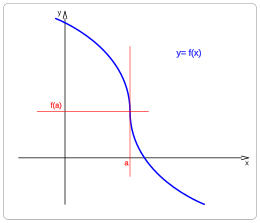
- Función continua y derivable en a
- Función decreciente para x < a.
- Función decreciente para x > a.
- Función decreciente en a.
- Para x < a la función es cóncava.
- Para x > a la función es convexa.
- Para x = a punto de inflexión vertical.
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.













