数学中，特别是在调和分析与拓扑群的理论中，庞特里雅金对偶定理是局部紧阿贝尔群之间的对偶，解释了傅里叶变换的一般性质。它统合了实数线上或有限阿贝尔群上的一些结果，如：

• 实数线上够“好”的复数值周期函数能表成傅里叶级数，反之也能从傅里叶级数推出原函数。
• 实数线上够“好”的复数值函数有傅里叶变换；一如周期函数，在此也能从其傅里叶变换反推出原函数。
• 有限阿贝尔群上的复数值函数有离散傅里叶变换，这是在对偶群上的函数。此外，也从离散傅里叶变换反推原函数。

局部紧阿贝尔群如圆群（模1复数的乘法群）、有限阿贝尔群（具有离散拓扑）、整数的加法群（具有离散拓扑）、实数，以及在实数或P进数域上的有限维向量空间。庞特里亚金对偶将傅立叶变换推广到所有此类群。局部紧阿贝尔群的庞特里亚金对偶是局部紧阿贝尔拓扑群，由群到圆群的连续群同态形成，具有点乘与紧集上一致收敛的拓扑。庞特里亚金对偶定理指出任何局部紧阿贝尔群与其二阶对偶群自然同构，傅里叶变换是定理的特例。

此理论由庞特里亚金（Lev Pontryagin）首开，并结合了约翰·冯·诺伊曼与安德烈·韦伊的哈尔测度理论，它依赖于局部紧阿贝尔群的对偶群理论。

庞特里亚金对偶性将有关实数线或有限阿贝尔群上函数的一系列观察置于统一的背景中：

• 实数线上，适当正则的复数值周期函数具有傅里叶级数，反之也能从傅里叶级数中推出原函数；
• 实数线上，适当正则的复数值函数具有傅里叶变换，结果也是实数线上的函数，且反之也能从傅里叶展开中推出原函数；
• 有限阿贝尔群上的复数值函数具有离散傅里叶变换，是对偶群上的函数，对偶群是（非规范）同构群。此外，有限阿贝尔群上的任何函数都能从离散傅里叶变换的结果中推出原函数。

这类似于向量空间的对偶向量空间：有限维向量空间V及其对偶向量空间${\displaystyle V^{*))$不是自然同构的，但其中一个的自同态代数（矩阵代数）同构于另一个的自同态代数的反环：${\displaystyle {\text{End))(V)\cong ((\text{End))(V^{*})}^{\text{op)),}$由转置。相似地，群G及其对偶群${\displaystyle {\widehat {G))}$一般不同构，但其自同态环是彼此的反环：${\displaystyle {\text{End))(G)\cong {\text{End))({\widehat {G)))^{\text{op))}$。更广义地看，这不仅仅是自同态代数的同构，而且是范畴的反变等价。

若拓扑群的底拓扑空间是局部紧豪斯多夫空间，则称其为局部紧群；若拓扑群的底群是阿贝尔群，则称拓扑群也是阿贝尔的。一个拓扑群${\displaystyle G}$被称作局部紧的，当且仅当其单位元e有个紧邻域。明白地说，这代表存在一个包含e的开集${\displaystyle V}$，使得它在${\displaystyle G}$里的闭包${\displaystyle {\bar {V))}$是紧的。 局部紧阿贝尔群的例子如：

• ${\displaystyle \mathbb {R} ^{n))$，配上向量加法。
• 正实数配上乘法。此群透过指数及对数映射同构于${\displaystyle \mathbb {R} }$。
• 任意赋以离散拓扑的有限阿贝尔群。根据有限阿贝尔群的结构定理，任何这样的群都是循环群的直积。
• 整数${\displaystyle \mathbb {Z} }$配上加法，并赋予离散拓扑。
• 圆群${\displaystyle \mathbb {T} }$。这是绝对值为一的复数在乘法下构成的群。我们有同构${\displaystyle \mathbb {T} \cong \mathbb {R} /\mathbb {Z} }$。
• p进数配上加法及其p进拓扑。

局部紧阿贝尔群G，G的特征标是一个从${\displaystyle G}$到圆群${\displaystyle \mathbb {T} }$的连续群同态；特征标在逐点乘法下构成一个群，一个特征标的逆元是它的复共轭。可证明所有${\displaystyle G}$上的特征标在紧致开拓扑（即：以紧集上的一致收敛定义收敛性）下构成一个局部紧致阿贝尔群，称作对偶群，记为${\displaystyle {\widehat {G))}$或${\displaystyle G^{\wedge ))$。即 $${\displaystyle {\widehat {G)):=\operatorname {Hom} (G,T).}$$ 庞特里亚金对偶${\displaystyle {\widehat {G))}$通常被赋予紧集上一致收敛给出的拓扑（即所有从G到T的连续函数空间上的紧开拓扑诱导的拓扑）。

例如，$${\displaystyle {\widehat {\mathbb {Z} /n\mathbb {Z} ))=\mathbb {Z} /n\mathbb {Z} ,\ {\widehat {\mathbb {Z} ))=T,\ {\widehat {\mathbb {R} ))=\mathbb {R} ,\ {\widehat {T))=\mathbb {Z} .}$$ 若${\displaystyle G}$可分，则${\displaystyle {\hat {G))}$可度量化，对一般的${\displaystyle G}$则不尽然。

在此，“自然”或“典范”同构意谓一个“自然地”定义的映射${\displaystyle G\rightarrow G^{\wedge \wedge ))$，要点是它在范畴中满足函子性（详见条目范畴论）。举例明之：任何有限阿贝尔群都同构于其对偶群，但并不存在典范同构。${\displaystyle x\in G}$上的自然同构定义如下：

$${\displaystyle x\mapsto \{\chi \mapsto \chi (x)\}{\mbox{ i.e. ))x(\chi ):=\chi (x)}$$。即$${\displaystyle \operatorname {ev} _{G}(x):(\chi \mapsto \chi (x)).}$$

换言之，我们借着将一个元素${\displaystyle x\in G}$在每个${\displaystyle G}$的特征上求值，得到一个${\displaystyle {\hat {G))}$上的特征。也就是说，群元素x与对偶上的求值特征（evaluation character）相等。这可用线性代数中的对偶空间来类比，就像一个布于${\displaystyle K}$的向量空间${\displaystyle V}$有对偶空间${\displaystyle \mathrm {Hom} (V,K)}$，对偶群可看成${\displaystyle \mathrm {Hom} (G,\mathbb {T} )}$。更抽象的说，这两者都是可表函子，被${\displaystyle K}$及${\displaystyle \mathbb {T} }$所表示。若G是有限阿贝尔群，则${\displaystyle G\cong {\widehat {G))}$，但这种同构并不规范。精确表述一般要考虑群的对偶，还要考虑群之间的映射，以将对偶当做函子，证明恒等函子与对偶函子不自然等价。对偶定理还意味着，对任何群（不一定是有限群），对偶函子是正合函子。

局部紧群${\displaystyle G}$最值得注意的性质之一是它带有一个唯一的自然测度，称作哈尔测度，这使得我们可以一致地为${\displaystyle G}$中“够好”的子集测量大小；在此“够好”的明确意义是博雷尔集，即由紧集生成的σ-代数中的一个元素。更明确地说，局部紧群${\displaystyle G}$的一个右哈尔测度是定义在G的博雷尔集上的可数可加度量μ，对于G的元素x和G的博雷尔子集A而言，${\displaystyle \mu (Ax)=\mu (A)}$是右不变的；此测度尚须满足一些正则性（详见主条目哈尔测度）。任两个右不变哈尔测度至多差一个正的比例常数。准此要领，亦可定义左不变哈尔测度，当${\displaystyle G}$是阿贝尔群时两者符应。

此测度让我们得以定义${\displaystyle G}$上的（复数值）博雷尔函数的积分，特别是可以考虑相关的${\displaystyle L^{p))$空间： $${\displaystyle {\mathcal {L))_{\mu }^{p}(G)=\left\{(f:G\to \mathbb {C} )\ {\Big |}\ \int _{G}|f(x)|^{p}\ d\mu (x)<\infty \right\}.}$$

注意，由于G上任意两哈尔测度都仅相差一个缩放因子，所以这个${\displaystyle L^{p))$-空间与哈尔测度的选择无关，可以写作${\displaystyle L^{p}(G)}$。然而，空间上的${\displaystyle L^{p))$-范数取决于哈尔测度的选择，因此若要讨论等距，就必须跟踪所使用的哈尔测度。

在整数对加法形成的无穷循环群${\displaystyle \mathbb {Z} }$ （配上离散拓扑）上，设χ为一特征，则${\displaystyle \chi (n)=\chi (1)^{n))$，因此χ决定于χ(1)的值；反之，给定一个${\displaystyle \alpha \in \mathbb {T} }$，必存在特征χ使得χ(1)=α，由此得到群同构${\displaystyle \mathbb {Z} ^{\wedge }{\stackrel {\sim }{\rightarrow ))\mathbb {T} }$。此外也容易验证${\displaystyle \mathbb {Z} ^{\wedge ))$上的紧-开拓扑对应到${\displaystyle \mathbb {T} }$诱导自${\displaystyle \mathbb {C} }$的拓扑。

因此，${\displaystyle \mathbb {Z} }$的对偶群自然地同构于${\displaystyle \mathbb {T} }$。

反之，${\displaystyle \mathbb {T} }$上的特征皆形如${\displaystyle z\mapsto z^{n))$，其中n是整数。由于${\displaystyle \mathbb {T} }$是紧的，其对偶群上的拓扑由一致收敛性给出，对应的不外是${\displaystyle \mathbb {Z} }$上的离散拓扑。因此${\displaystyle \mathbb {T} }$的对偶群自然地同构于${\displaystyle \mathbb {Z} }$。

实数对加法构成的群${\displaystyle \mathbb {R} }$同构于自身的对偶群；${\displaystyle \mathbb {R} }$上的特征皆形如${\displaystyle r\mapsto e^{ir))$，其中r是实数。借着这些对偶性，下节描述的傅里叶变换将符应于${\displaystyle \mathbb {R} }$上的古典版本。

局部紧阿贝尔群的对偶群被用作傅里叶变换的底空间（即变换的值域）。设${\displaystyle f\in L^{1}(G)}$，则傅里叶变换就是${\displaystyle {\widehat {G))}$上的函数${\displaystyle {\widehat {f))}$，定义为

$${\displaystyle {\widehat {f))(\chi )=\int _{G}f(x){\overline {\chi (x)))\ d\mu (x),}$$ 其中积分是对于G上的哈尔测度${\displaystyle \mu }$，这也记作${\displaystyle ({\mathcal {F))f)(\chi )}$。注意傅里叶变换取决于哈尔测度的选择。不难证明，${\displaystyle {\widehat {f))}$是${\displaystyle {\widehat {G))}$上的有界连续函数，在无穷远处趋近于零。

${\displaystyle {\widehat {G))}$上可积函数的傅里叶反变换由下式给出 $${\displaystyle {\check {g))(x)=\int _{\widehat {G))g(\chi )\chi (x)\ d\nu (\chi ),}$$ 其中积分是对于对偶群${\displaystyle {\widehat {G))}$上的哈尔测度${\displaystyle \nu }$。傅里叶反变换公式中所见${\displaystyle {\widehat {G))}$上的测度${\displaystyle \nu }$称作${\displaystyle \mu }$的对偶测度，可记作${\displaystyle {\widehat {\mu ))}$

各种傅里叶变换可按其域和变换域（群与对偶群）分类如下（注意${\displaystyle \mathbb {T} }$是圆群）：

变换	原域G	变换域${\displaystyle {\hat {G))}$	测度${\displaystyle \mu }$
傅里叶变换	${\displaystyle \mathbb {R} }$	${\displaystyle \mathbb {R} }$	常数${\displaystyle \times }$勒贝格测度
傅里叶级数	${\displaystyle \mathbb {T} }$	${\displaystyle \mathbb {Z} }$	常数${\displaystyle \times }$勒贝格测度
离散时间傅里叶变换 (DTFT)	${\displaystyle \mathbb {Z} }$	${\displaystyle \mathbb {T} }$	常数${\displaystyle \times }$计数测度
离散傅里叶变换 (DFT)	${\displaystyle \mathbb {Z} _{n))$	${\displaystyle \mathbb {Z} _{n))$	常数${\displaystyle \times }$计数测度

例如，设${\displaystyle G=\mathbb {R} ^{n))$，就可以通过配对${\displaystyle (\mathbf {v} ,\mathbf {w} )\mapsto e^{i\mathbf {v} \cdot \mathbf {w} ))$将${\displaystyle {\widehat {G))}$想象成${\displaystyle \mathbb {R} ^{n))$。若${\displaystyle \mu }$是欧氏空间上的勒贝格测度，就可得到${\displaystyle \mathbb {R} ^{n))$上的普通傅里叶变换，反变换所需的对偶测度则是${\displaystyle {\widehat {\mu ))=(2\pi )^{-n}\mu }$。若要得到两侧测度相同的傅里叶反变换公式（即，既然可以将${\displaystyle \mathbb {R} ^{n))$视作自身的对偶空间，也可以设${\displaystyle {\widehat {\mu ))=\mu }$），则需要用

$${\displaystyle {\begin{aligned}\mu &=(2\pi )^{-{\frac {n}{2))}\times {\text{Lebesgue measure))\\{\widehat {\mu ))&=(2\pi )^{-{\frac {n}{2))}\times {\text{Lebesgue measure))\end{aligned))}$$

然而，若把${\displaystyle \mathbb {R} ^{n))$与其对偶群相等的判断方法改为配对 $${\displaystyle (\mathbf {v} ,\mathbf {w} )\mapsto e^{2\pi i\mathbf {v} \cdot \mathbf {w} },}$$ 则${\displaystyle \mathbb {R} ^{n))$上的勒贝格测度等于其自身的对偶测度。计算欧氏空间上的傅里叶变换或傅里叶反变换时，这个约定可最大限度地减少各处出现的${\displaystyle 2\pi }$数量（实际上，它将${\displaystyle 2\pi }$仅限制在指数上，而非作为积分符号之外的预因子）。注意，如何确定${\displaystyle \mathbb {R} ^{n))$等于其对偶群会影响“自对偶函数”的含义，其是${\displaystyle \mathbb {R} ^{n))$上等同于自身的傅里叶变换的函数：使用经典配对${\displaystyle (\mathbf {v} ,\mathbf {w} )\mapsto e^{i\mathbf {v} \cdot \mathbf {w} ))$，函数${\displaystyle e^{-{\frac {1}{2))x^{2))}$是自对偶的。但配对可以保持预因子统一，${\displaystyle (\mathbf {v} ,\mathbf {w} )\mapsto e^{2\pi i\mathbf {v} \cdot \mathbf {w} ))$使得${\displaystyle e^{-\pi x^{2))}$自对偶。这傅里叶变换的第二个定义的优点在于，它将乘法单位元映射为卷积单位元，由于${\displaystyle L^{1))$是卷积代数，这一点非常有用。另外，此形式在${\displaystyle L^{2))$空间上也必等距。

局部紧阿贝尔群${\displaystyle G}$上的可积函数构成一个代数，其乘法是卷积：设${\displaystyle f,g\in L^{1}(G)}$，则卷积定义为

${\displaystyle [f\star g](x)=\int _{G}f(x-y)g(y)\,d\mu (y)}$。

此代数称作${\displaystyle G}$的群代数。根据富比尼-托内利定理，卷积对${\displaystyle L^{1))$范数是次乘法，因此${\displaystyle L^{1}(G)}$是个巴拿赫代数。巴拿赫代数${\displaystyle L^{1}(G)}$一般没有乘法单位元，除非${\displaystyle G}$离散，即在单位元处为1、他处为0的函数。但它有个近似单位元，这是个网，以一有向集${\displaystyle I}$为索引，写作${\displaystyle (e_{i})_{i\in I))$并满足${\displaystyle f\star e_{i}\rightarrow f}$。

傅里叶变换将卷积映至逐点乘法，即它是（范数≤ 1的）阿贝尔巴拿赫代数的同态${\displaystyle L^{1}(G)\to C_{0}\left({\widehat {G))\right)}$：

$${\displaystyle {\mathcal {F))(f\star g)(\chi )={\mathcal {F))(f)(\chi )\cdot {\mathcal {F))(g)(\chi )}$$。 特别是，${\displaystyle G}$上的任意特征χ，都可在群代数上确定唯一的积性线性泛函 $${\displaystyle f\mapsto {\widehat {f))(\chi )}$$。

群代数的重要性质之一，在于这些线性泛函穷竭了群代数上所有非平凡（即：非恒零）的积性线性泛函。见文献中Loomis著作的第34节。这意味着傅里叶变换是盖尔范德变换的特例。

如前所述，一个局部紧阿贝尔群${\displaystyle G}$的对偶群依然是局部紧阿贝尔群，因而带有一族哈尔测度，彼此至多差一个比例常数。

由于G上紧支的复值连续函数是${\displaystyle L^{2))$-稠密的，因此从该空间到幺正算符的傅里叶变换有唯一的扩展

$${\displaystyle {\mathcal {F)):L_{\mu }^{2}(G)\to L_{\nu }^{2}\left({\widehat {G))\right).}$$ 且有 $${\displaystyle \forall f\in L^{2}(G):\quad \int _{G}|f(x)|^{2}\ d\mu (x)=\int _{\widehat {G))\left|{\widehat {f))(\chi )\right|^{2}\ d\nu (\chi ).}$$

注意，若${\displaystyle G}$非紧，${\displaystyle L^{1}(G)}$并不包含${\displaystyle L^{2}(G)}$，所以G上一般${\displaystyle L^{2))$-函数的傅里叶变换不由任何积分公式（或任何明确公式）给出。要定义${\displaystyle L^{2))$-函数的傅里叶变换，就须诉诸一些技巧，例如限制于一个稠密子空间，如具有紧支的连续函数，然后通过连续性将等距性扩展到整个空间。

依循Loomis书中术语，我们称一对${\displaystyle G}$与其对偶群上的哈尔测度${\displaystyle (\mu ,\nu )}$是相系的，当且仅当傅里叶反转公式成立。傅里叶变换之幺正性遂蕴含：对所有${\displaystyle G}$上的连续紧支集复数值函数${\displaystyle f}$都有

${\displaystyle \int _{G}|f(x)|^{2}\ d\mu (x)=\int _{\widehat {G))|{\widehat {f))(\chi )|^{2}\ d\nu (\chi )}$

在平方可积函数空间上，我们考虑的傅里叶变换是透过上述幺正延拓得到的算子。对偶群本身也有个傅里叶逆变换；它可以刻划为${\displaystyle L^{2))$傅里叶变换之逆（或其伴随算子，因为傅里叶变换是幺正的），这是以下傅里叶反转公式的内涵。

• 在${\displaystyle G=\mathbb {T} }$的情形，对偶群${\displaystyle {\widehat {G))}$自然同构于整数群${\displaystyle \mathbb {Z} }$，傅里叶变换专门用于计算周期函数的傅里叶级数系数。
• 在${\displaystyle G=\mathbb {R} ^{n))$的情形，我们有${\displaystyle {\hat {G))=\mathbb {R} ^{n))$，若取下述相系的哈尔测度，则回到傅里叶变换的古典定义：

$${\displaystyle \mu =(2\pi )^{-n/2}\times }$$（勒贝格测度） $${\displaystyle \nu =(2\pi )^{-n/2}\times }$$（勒贝格测度）

• 在${\displaystyle G=\mathbb {T} }$的情形，对偶群${\displaystyle {\hat {G))}$自然同构于${\displaystyle \mathbb {Z} }$，而上述算子${\displaystyle F}$归于计算周期函数的傅里叶系数。
• 若${\displaystyle G}$为有限群，则得到离散傅里叶变换。此情形易直接证明。

庞特里亚金对偶定理的重要应用之一是下述关于紧阿贝尔拓扑群的刻划：

G的紧的，意味着${\displaystyle {\widehat {G))}$是离散的或紧的，这是${\displaystyle {\widehat {G))}$上紧-开拓扑定义的一个基本结果，不需要庞特里亚金对偶性。我们可以利用庞特里亚金对偶性证明相反情形。

对任何拓扑群，无论局部紧或阿贝尔与否，皆可定义玻尔紧化。利用紧阿贝尔群和离散阿贝尔群之间的庞特里亚金对偶性，可描述任意阿贝尔局部紧拓扑群的玻尔紧化。G的玻尔紧化${\displaystyle B(G)}$是${\displaystyle {\widehat {H))}$，其中H具有群结构${\displaystyle {\widehat {G))}$，但带离散拓扑。由于下述包含映射 $${\displaystyle \iota :H\to {\widehat {G))}$$ 是个连续同态，其对偶同态 $${\displaystyle G\sim {\widehat {\widehat {G))}\to {\widehat {H))}$$ 是个映至一个紧群的同态；可以证明它满足必要的泛性质，因而${\displaystyle {\hat {H))}$确为${\displaystyle G}$的玻尔紧化。

函子的观点对于研究对偶群是很有用的。以下将以LCA表示所有局部紧阿贝尔群及其间的连续群同态构成之范畴。

对偶群的构造${\displaystyle G\mapsto {\widehat {G))}$给出一个反变函子${\displaystyle \mathbf {LCA} \rightarrow \mathbf {LCA} }$，（在可表函子的意义上）由圆群${\displaystyle \mathbb {T} }$表为${\displaystyle {\widehat {G))={\text{Hom))(G,\mathbb {T} )}$。其二次迭代${\displaystyle G\mapsto G^{\wedge \wedge ))$遂给出协变函子${\displaystyle \mathbf {LCA} \rightarrow \mathbf {LCA} }$。

庞特里亚金对偶性的一个范畴论表述是，LCA上的恒等函子与二阶对偶函子之间的自然变换同构。^[3]从自然变换的角度看，这意味着映射${\displaystyle G\to \operatorname {Hom} (\operatorname {Hom} (G,T),T)}$对任何局部紧阿贝尔群G都是同构，且它们在G中是函子。此同构可以类比于有限维向量空间的二次对偶（特别是实与复向量空间）。

这种表述的直接结果是庞特里亚金对偶的另一种常见范畴论表述：对偶群函子是${\displaystyle \mathbf {LCA} \rightarrow \mathbf {LCA} ^{\text{op))}$的范畴等价。 庞特里亚金对偶性将离散群与紧群的子范畴交换。若${\displaystyle R}$是一个环，而${\displaystyle G}$是个左${\displaystyle R}$-模，则对偶群${\displaystyle {\widehat {G))}$将成为右${\displaystyle R}$-模。从对偶性可推知离散左${\displaystyle R}$-模与紧右${\displaystyle R}$-模对偶。LCA里的自同态环${\displaystyle \mathrm {End} (G)}$依对偶性对应至其反环（即：环的乘法次序交换）。举例明之：取有限循环离散群${\displaystyle G=\mathbb {Z} }$，则${\displaystyle {\widehat {G))=\mathbb {T} }$；前者满足${\displaystyle \mathrm {End} (G)=\mathbb {Z} }$，对后者亦然。

庞特里亚金对偶的推广有两个主要方向：非局部紧的交换拓扑群，和非交换拓扑群。这两种情形的理论截然不同。

若G是豪斯多夫阿贝尔拓扑群，则具有紧-开拓扑的${\displaystyle {\widehat {G))}$ 也是豪斯多夫阿贝尔拓扑群，G到二阶对偶${\displaystyle {\widehat {\widehat {G))))$的自然映射有意义。若此映射是同构，就可以说G满足庞特里亚金对偶性（或称G是${\displaystyle G}$反身群（reflexive group）^[4]或反射群（reflective group）^[5]）。除了G为局部紧群的情形，这个问题还在很多方向上得到扩展。^[6]

Samuel Kaplan^[7][8]在1948年和1950年证明，局部紧（豪斯多夫）阿贝尔群的任意积和可数反极限满足庞特里亚金对偶性。注意，局部紧非紧空间的无限积不是局部紧的。

Rangachari Venkataraman (1975)^[9]证明，除其他事实外，满足庞特里亚金对偶性的阿贝尔拓扑群的每个开子群都满足庞特里亚金对偶性。

最近，Sergio Ardanza-Trevijano和María Jesús Chasco^[10]扩展了上述结果，证明只要满足一些额外条件，满足庞特里亚金对偶性的阿贝尔群序列的直极限和反极限也满足庞特里亚金对偶性，条件是群须可度量化，或是${\displaystyle k_{\omega ))$-空间，但不必是局部紧的。

但若要考虑局部紧情形之外的庞特里亚金对偶性，就会有根本性的变化。Elena Martín-Peinador (1995)^[11]证明，若G是满足庞特里亚金对偶性的豪斯多夫拓扑群，且自然求值对 $${\displaystyle {\begin{cases}G\times {\widehat {G))\to \mathbb {T} \\(x,\chi )\mapsto \chi (x)\end{cases))}$$ （联合）连续，^[a]则G是局部紧的。有推论，庞特里亚金对偶性的所有非局部紧例子都是配对${\displaystyle G\times {\widehat {G))\to \mathbb {T} }$不（联合）连续的群。

另一种将对偶性推广到其他类的交换拓扑群的方法是赋予对偶群${\displaystyle {\widehat {G))}$以一点不同的拓扑，即全有界集上的均匀收敛拓扑。在此假设下，满足等式${\displaystyle G\cong {\widehat {\widehat {G))))$的群^[b]称作刻板群（stereotype groups）。^[5]这类群的范围很广（包含局部紧阿贝尔群），但比反射群要窄。^[5]

Marianne F. Smith (1952)^[12]注意到，巴拿赫空间和自反空间被视作拓扑群（加法为群运算），且满足庞特里亚金对偶性。之后B. S. Brudovskiĭ^[13]、William C. Waterhouse^[14]及K. Brauner^[15]证明，这一结果可推广到所有准全桶型空间类（尤其是所有弗雷歇空间）。1990年代，Sergei Akbarov^[16]描述了一类拓扑向量空间。满足比经典庞特里亚金反射更强的性质，即等式 $${\displaystyle (X^{\star })^{\star }\cong X}$$ 其中${\displaystyle X^{\star ))$表示在X中被赋以全有界集上一致收敛拓扑的所有线性连续泛函${\displaystyle f\colon X\to \mathbb {C} }$的空间（${\displaystyle (X^{\star })^{\star ))$是相同意义上${\displaystyle X^{\star ))$的对偶）。这类空间称作刻板空间（stereotype space），相应理论在泛函分析与几何中得到一系列应用，包括庞特里亚金对偶性在非交换拓扑群中的推广。

对非交换群${\displaystyle G}$没有类似的理论，因为此时对偶的对象${\displaystyle {\hat {G))}$={${\displaystyle G}$的不可约表示之同构类}不只有一维表示，因此不构成一个群。同时，G的不可约酉表示集上如何引入惩罚也不清楚，甚至不清楚这个集合是否适合作为G的对偶对象。因此，这种情况下构造对偶性的问题需要彻底重新思考。

迄今建立的理论主要有两类：一类理论中，对偶对象与原对象具有相同性质（如庞特里亚金对偶理论），一类理论中，对偶对象与原对象存在根本差异，以至于无法将它们视作一类对象。第二类理论出现得更早：在庞特里亚金的研究后不久，淡中忠郎 (1938)和马克·克林 (1949)构建了任意紧群的对偶论，即现在所谓淡中-克林对偶性。^[17][18]此理论中，群G的对偶对象不是群，而是其表示的范畴${\displaystyle \Pi (G)}$。但它缺乏与调和分析的联系，因而无法处理关于${\displaystyle {\hat {G))}$上的普朗歇尔测度的问题。

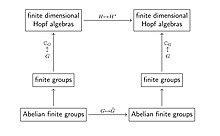
第一类理论是后来出现的，它们的主要例子是有限群的对偶论。^[19][20]其中，有限群范畴通过（在${\displaystyle \mathbb {C} }$上）取群代数${\displaystyle \mathbb {C} _{G))$的运算${\displaystyle G\mapsto \mathbb {C} _{G))$嵌入到有限维霍普夫代数范畴中，这样庞特里亚金对偶函子${\displaystyle G\mapsto {\widehat {G))}$就变为取对偶向量空间的运算${\displaystyle H\mapsto H^{*))$（这是有限维霍普夫代数范畴中的对偶函子）。^[20]

1973年，Leonid I. Vainerman、George I. Kac、Michel Enock、Jean-Marie Schwartz为所有局部紧群构造了这种类型的一般理论。^[21]1980年代起，量子群的发现使这一领域的研究复兴了，构建的理论开始得到积极的移植。^[22]这些理论的用C*-代数或冯诺依曼代数的语言描述的，其变体之一是最近的局部紧量子群理论。^[23][22]

这些一般理论的一个缺点是，推广群概念的对象不是通常代数意义上的霍普夫代数。^[20]这一缺陷可在拓扑代数的包络为基础的对偶理论框架内得到纠正（仅对一部分类别的群）。^[24]

庞特里亚金在1934年为局部紧阿贝尔群及其对偶性的理论奠下基础。他的进路须假定群是第二可数的，并且是紧群或离散群。此条件先后由E.R. van Kampen（1935年）与安德鲁·韦伊（1953年）改进为局部紧阿贝尔群。

下列书籍（可在大部分大学图书馆找到）都有局部紧阿贝尔群、对偶定理与傅里叶变换的相关章节。Dixmier的著作有非交换调和分析的材料，也有英译本。

• Jacques Dixmier, Les C*-algèbres et leurs Représentations, Gauthier-Villars,1969.
• Lynn H. Loomis, An Introduction to Abstract Harmonic Analysis, D. van Nostrand Co, 1953
• Walter Rudin, Fourier Analysis on Groups, 1962
• Hans Reiter, Classical Harmonic Analysis and Locally Compact Groups, 1968（2nd ed produced by Jan D. Stegeman, 2000）。
• Hewitt and Ross, Abstract Harmonic Analysis, vol 1, 1963.

• 彼得-魏尔定理
• 卡地亚对偶性

• Akbarov, S.S. Pontryagin duality in the theory of topological vector spaces and in topological algebra. Journal of Mathematical Sciences. 2003, 113 (2): 179–349. S2CID 115297067. doi:10.1023/A:1020929201133 . 
• Akbarov, Sergei S.; Shavgulidze, Evgeniy T. On two classes of spaces reflexive in the sense of Pontryagin. Matematicheskii Sbornik. 2003, 194 (10): 3–26. 
• Akbarov, Sergei S. Holomorphic functions of exponential type and duality for Stein groups with algebraic connected component of identity. Journal of Mathematical Sciences. 2009, 162 (4): 459–586. S2CID 115153766. arXiv:0806.3205 . doi:10.1007/s10958-009-9646-1. 
• Akbarov, Sergei S. Continuous and smooth envelopes of topological algebras. Part 1. Journal of Mathematical Sciences. 2017a, 227 (5): 531–668. MR 3790317. S2CID 126018582. arXiv:1303.2424 . doi:10.1007/s10958-017-3599-6. 
• Akbarov, Sergei S. Continuous and smooth envelopes of topological algebras. Part 2. Journal of Mathematical Sciences. 2017b, 227 (6): 669–789. MR 3796205. S2CID 128246373. arXiv:1303.2424 . doi:10.1007/s10958-017-3600-4. 
• Brauner, Kalman. Duals of Fréchet spaces and a generalization of the Banach–Dieudonné theorem. Duke Mathematical Journal. 1973, 40 (4): 845–855. doi:10.1215/S0012-7094-73-04078-7. 
• Brudovskiĭ, B. S. On k- and c-reflexivity of locally convex vector spaces. Lithuanian Mathematical Journal. 1967, 7 (1): 17–21. doi:10.15388/LMJ.1967.19927 . 
• Dixmier, Jacques. Les C*-algèbres et leurs Représentations. Gauthier-Villars. 1969. ISBN 978-2-87647-013-2. 
• Enock, Michel; Schwartz, Jean-Marie. Kac Algebras and Duality of Locally Compact Groups. With a preface by Alain Connes. With a postface by Adrian Ocneanu. Berlin: Springer-Verlag. 1992. ISBN 978-3-540-54745-7. MR 1215933. doi:10.1007/978-3-662-02813-1. 
• Hewitt, Edwin; Ross, Kenneth A. Abstract Harmonic Analysis. Vol. I: Structure of topological groups. Integration theory, group representations. Die Grundlehren der mathematischen Wissenschaften 115. Berlin-Göttingen-Heidelberg: Springer-Verlag. 1963. ISBN 978-0-387-94190-5. MR 0156915. 
• Hewitt, Edwin; Ross, Kenneth A. Abstract Harmonic Analysis 2. Springer. 1970. ISBN 978-3-662-24595-8. MR 0262773. 
• Kirillov, Alexandre A. Elements of the theory of representations. Grundlehren der Mathematischen Wissenschaften 220. Berlin, New York: Springer-Verlag. 1976 [1972]. ISBN 978-0-387-07476-4. MR 0412321. 
• Loomis, Lynn H. An Introduction to Abstract Harmonic Analysis. D. van Nostrand Co. 1953. ISBN 978-0486481234. 
• Morris, S.A. Pontryagin duality and the structure of locally compact Abelian groups. Cambridge University Press. 1977. ISBN 978-0521215435. 
• Onishchik, A.L., Pontrjagin duality, Encyclopedia of Mathematics, 1984, 4: 481–482, ISBN 978-1402006098 
• Reiter, Hans. Classical Harmonic Analysis and Locally Compact Groups. Clarendon Press. 1968. ISBN 978-0198511892. 
• Rudin, Walter. Fourier Analysis on Groups. D. van Nostrand Co. 1962. ISBN 978-0471523642. 
• Timmermann, T. An Invitation to Quantum Groups and Duality - From Hopf Algebras to Multiplicative Unitaries and Beyond. EMS Textbooks in Mathematics, European Mathematical Society. 2008. ISBN 978-3-03719-043-2. 
• Kustermans, J.; Vaes, S. Locally Compact Quantum Groups. Annales Scientifiques de l'École Normale Supérieure. 2000, 33 (6): 837–934. doi:10.1016/s0012-9593(00)01055-7. 
• Ardanza-Trevijano, Sergio; Chasco, María Jesús. The Pontryagin duality of sequential limits of topological Abelian groups. Journal of Pure and Applied Algebra. 2005, 202 (1–3): 11–21. MR 2163398. doi:10.1016/j.jpaa.2005.02.006. hdl:10171/1586 . 
• Chasco, María Jesús; Dikranjan, Dikran; Martín-Peinador, Elena. A survey on reflexivity of abelian topological groups. Topology and Its Applications. 2012, 159 (9): 2290–2309. MR 2921819. doi:10.1016/j.topol.2012.04.012 . 
• Kaplan, Samuel. Extensions of the Pontrjagin duality. Part I: infinite products. Duke Mathematical Journal. 1948, 15: 649–658. MR 0026999. doi:10.1215/S0012-7094-48-01557-9. 
• Kaplan, Samuel. Extensions of the Pontrjagin duality. Part II: direct and inverse limits. Duke Mathematical Journal. 1950, 17: 419–435. MR 0049906. doi:10.1215/S0012-7094-50-01737-6. 
• Venkataraman, Rangachari. Extensions of Pontryagin Duality. Mathematische Zeitschrift. 1975, 143 (2): 105–112. S2CID 123627326. doi:10.1007/BF01187051. 
• Martín-Peinador, Elena. A reflexible admissible topological group must be locally compact. Proceedings of the American Mathematical Society. 1995, 123 (11): 3563–3566. JSTOR 2161108. doi:10.2307/2161108. hdl:10338.dmlcz/127641 . 
• Roeder, David W. Category theory applied to Pontryagin duality. Pacific Journal of Mathematics. 1974, 52 (2): 519–527. doi:10.2140/pjm.1974.52.519 . 
• Smith, Marianne F. The Pontrjagin duality theorem in linear spaces. Annals of Mathematics. 1952, 56 (2): 248–253. JSTOR 1969798. MR 0049479. doi:10.2307/1969798. 
• Waterhouse, William C. Dual groups of vector spaces. Pacific Journal of Mathematics. 1968, 26 (1): 193–196. doi:10.2140/pjm.1968.26.193 .