Гиперболи́ческие фу́нкции — семейство элементарных функций , выражающихся через экспоненту и тесно связанных с тригонометрическими функциями .
sh
x
{\displaystyle \operatorname {sh} x}
ch
x
{\displaystyle \operatorname {ch} x}
Гиперболические функции задаются следующими формулами:
sh
x
=
e
x
−
e
−
x
2
{\displaystyle \operatorname {sh} x={\frac {e^{x}-e^{-x)){2))}
(в англоязычной литературе обозначается
sinh
x
{\displaystyle \sinh x}
ch
x
=
e
x
+
e
−
x
2
{\displaystyle \operatorname {ch} x={\frac {e^{x}+e^{-x)){2))}
(в англоязычной литературе обозначается
cosh
x
{\displaystyle \cosh x}
th
x
=
sh
x
ch
x
=
e
x
−
e
−
x
e
x
+
e
−
x
=
e
2
x
−
1
e
2
x
+
1
{\displaystyle \operatorname {th} x={\frac {\operatorname {sh} x}{\operatorname {ch} x))={\frac {e^{x}-e^{-x)){e^{x}+e^{-x))}={\frac {e^{2x}-1}{e^{2x}+1))}
(в англоязычной литературе обозначается
tanh
x
{\displaystyle \tanh x}
гиперболический котангенс :
cth
x
=
1
th
x
=
ch
x
sh
x
=
e
x
+
e
−
x
e
x
−
e
−
x
=
e
2
x
+
1
e
2
x
−
1
{\displaystyle \operatorname {cth} x={\frac {1}{\operatorname {th} x))={\frac {\operatorname {ch} x}{\operatorname {sh} x))={\frac {e^{x}+e^{-x)){e^{x}-e^{-x))}={\frac {e^{2x}+1}{e^{2x}-1))}
(в англоязычной литературе обозначается
coth
x
{\displaystyle \coth x}
sch
x
=
1
ch
x
=
2
e
x
+
e
−
x
{\displaystyle \operatorname {sch} x={\frac {1}{\operatorname {ch} x))={\frac {2}{e^{x}+e^{-x))))
Гиперболический секанс иногда также обозначается как
sech
x
{\displaystyle \operatorname {sech} x}
гиперболический косеканс :
csch
x
=
1
sh
x
=
2
e
x
−
e
−
x
{\displaystyle \operatorname {csch} x={\frac {1}{\operatorname {sh} x))={\frac {2}{e^{x}-e^{-x))))
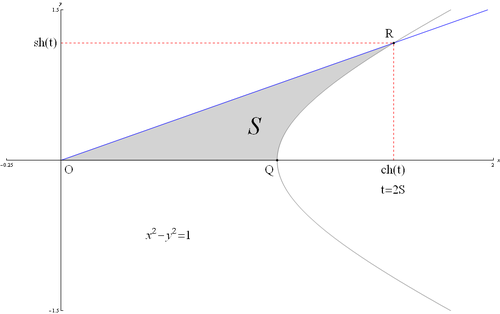
Определение гиперболических функций через гиперболу Параметризация гиперболического синуса (анимация). Ввиду соотношения
ch
2
t
−
sh
2
t
=
1
{\displaystyle \operatorname {ch} ^{2}t-\operatorname {sh} ^{2}t=1}
параметрическое представление гиперболы
x
2
−
y
2
=
1
{\displaystyle x^{2}-y^{2}=1}
x
=
ch
t
{\displaystyle x=\operatorname {ch} t}
y
=
sh
t
{\displaystyle y=\operatorname {sh} t}
t
=
2
S
{\displaystyle t=2S}
S
{\displaystyle S}
O
Q
R
{\displaystyle OQR}
O
X
{\displaystyle OX}
синуса в параметрической форме:
x
=
t
,
y
=
f
(
t
)
{\displaystyle x=t,y=f(t)}
f
(
t
)
{\displaystyle f(t)}
гиперболы , соответствующей вершине криволинейного треугольника площадью
S
=
t
/
2
{\displaystyle S=t/2}
окружность , которое тоже можно построить подобным образом.
Гиперболические функции выражаются через тригонометрические функции от мнимого аргумента.
sh
x
=
−
i
sin
(
i
x
)
,
ch
x
=
cos
(
i
x
)
,
th
x
=
−
i
tg
(
i
x
)
{\displaystyle \operatorname {sh} x=-i\sin(ix),\quad \operatorname {ch} x=\cos(ix),\quad \operatorname {th} x=-i\operatorname {tg} (ix)}
sh
(
i
x
)
=
i
sin
x
,
ch
(
i
x
)
=
cos
x
,
th
(
i
x
)
=
i
tg
x
{\displaystyle \operatorname {sh} (ix)=i\sin x,\quad \operatorname {ch} (ix)=\cos x,\quad \operatorname {th} (ix)=i\operatorname {tg} x}
Функция Гудермана связывает тригонометрические функции и гиперболические функции без привлечения комплексных чисел .
ch
2
x
−
sh
2
x
=
1.
{\displaystyle \operatorname {ch} ^{2}x-\operatorname {sh} ^{2}x=1.}
ch
2
x
−
sh
2
x
=
(
e
x
+
e
−
x
2
)
2
−
(
e
x
−
e
−
x
2
)
2
=
(
e
x
+
e
−
x
)
2
−
(
e
x
−
e
−
x
)
2
4
=
e
2
x
+
2
+
e
−
2
x
−
e
2
x
+
2
−
e
−
2
x
4
=
2
+
2
4
=
1
{\displaystyle \operatorname {ch} ^{2}x-\operatorname {sh} ^{2}x=\left({\frac {e^{x}+e^{-x)){2))\right)^{2}-\left({\frac {e^{x}-e^{-x)){2))\right)^{2}={\frac {(e^{x}+e^{-x})^{2}-(e^{x}-e^{-x})^{2)){4))={\frac {e^{2x}+2+e^{-2x}-e^{2x}+2-e^{-2x)){4))={\frac {2+2}{4))=1}
Чётность/нечётность :
sh
(
−
x
)
=
−
sh
x
.
{\displaystyle \operatorname {sh} (-x)=-\operatorname {sh} x.}
ch
(
−
x
)
=
ch
x
.
{\displaystyle \operatorname {ch} (-x)=\operatorname {ch} x.}
th
(
−
x
)
=
−
th
x
.
{\displaystyle \operatorname {th} (-x)=-\operatorname {th} x.}
cth
(
−
x
)
=
−
cth
x
.
{\displaystyle \operatorname {cth} (-x)=-\operatorname {cth} x.}
sch
(
−
x
)
=
sch
x
.
{\displaystyle \operatorname {sch} (-x)=\operatorname {sch} x.}
csch
(
−
x
)
=
−
csch
x
.
{\displaystyle \operatorname {csch} (-x)=-\operatorname {csch} x.}
Формулы сложения :
sh
(
x
±
y
)
=
sh
x
ch
y
±
sh
y
ch
x
.
{\displaystyle \operatorname {sh} (x\pm y)=\operatorname {sh} x\,\operatorname {ch} y\pm \operatorname {sh} y\,\operatorname {ch} x.}
ch
(
x
±
y
)
=
ch
x
ch
y
±
sh
y
sh
x
.
{\displaystyle \operatorname {ch} (x\pm y)=\operatorname {ch} x\,\operatorname {ch} y\pm \operatorname {sh} y\,\operatorname {sh} x.}
th
(
x
±
y
)
=
th
x
±
th
y
1
±
th
x
th
y
.
{\displaystyle \operatorname {th} (x\pm y)={\frac {\operatorname {th} x\pm \operatorname {th} y}{1\pm \operatorname {th} x\,\operatorname {th} y)).}
cth
(
x
±
y
)
=
1
±
cth
x
cth
y
cth
x
±
cth
y
.
{\displaystyle \operatorname {cth} (x\pm y)={\frac {1\pm \operatorname {cth} x\,\operatorname {cth} y}{\operatorname {cth} x\pm \operatorname {cth} y)).}
Формулы двойного аргумента:
sh
2
x
=
2
ch
x
sh
x
=
2
th
x
1
−
th
2
x
.
{\displaystyle \operatorname {sh} 2x=2\operatorname {ch} x\,\operatorname {sh} x={\frac {2\,\operatorname {th} x}{1-\operatorname {th} ^{2}x)).}
ch
2
x
=
ch
2
x
+
sh
2
x
=
2
ch
2
x
−
1
=
1
+
2
sh
2
x
=
1
+
th
2
x
1
−
th
2
x
.
{\displaystyle \operatorname {ch} 2x=\operatorname {ch} ^{2}x+\operatorname {sh} ^{2}x=2\operatorname {ch} ^{2}x-1=1+2\operatorname {sh} ^{2}x={\frac {1+\operatorname {th} ^{2}x}{1-\operatorname {th} ^{2}x)).}
th
2
x
=
2
th
x
1
+
th
2
x
.
{\displaystyle \operatorname {th} 2x={\frac {2\operatorname {th} x}{1+\operatorname {th} ^{2}x)).}
cth
2
x
=
1
2
(
th
x
+
cth
x
)
.
{\displaystyle \operatorname {cth} 2x={\frac {1}{2))(\operatorname {th} x+\operatorname {cth} x).}
th
x
=
ch
2
x
−
1
sh
2
x
=
sh
2
x
1
+
ch
2
x
.
{\displaystyle \operatorname {th} x={\frac {\operatorname {ch} 2x-1}{\operatorname {sh} 2x))={\frac {\operatorname {sh} 2x}{1+\operatorname {ch} 2x)).}
ch
2
x
±
sh
2
x
=
(
sh
x
±
ch
x
)
2
.
{\displaystyle \operatorname {ch} 2x\pm \operatorname {sh} 2x=(\operatorname {sh} x\pm \operatorname {ch} x)^{2}.}
Формулы кратных аргументов:
sh
3
x
=
4
sh
3
x
+
3
sh
x
.
{\displaystyle \operatorname {sh} 3x=4\operatorname {sh} ^{3}x+3\operatorname {sh} x.}
ch
3
x
=
4
ch
3
x
−
3
ch
x
.
{\displaystyle \operatorname {ch} 3x=4\operatorname {ch} ^{3}x-3\operatorname {ch} x.}
th
3
x
=
3
+
th
2
x
1
+
3
th
2
x
.
{\displaystyle \operatorname {th} 3x={\frac {3+\operatorname {th} ^{2}x}{1+3\operatorname {th} ^{2}x)).}
sh
5
x
=
16
sh
5
x
+
20
sh
3
x
+
5
sh
x
.
{\displaystyle \operatorname {sh} 5x=16\operatorname {sh} ^{5}x+20\operatorname {sh} ^{3}x+5\operatorname {sh} x.}
ch
5
x
=
16
ch
5
x
−
20
ch
3
x
+
5
ch
x
.
{\displaystyle \operatorname {ch} 5x=16\operatorname {ch} ^{5}x-20\operatorname {ch} ^{3}x+5\operatorname {ch} x.}
th
5
x
=
th
x
th
4
x
+
10
th
2
x
+
5
5
th
4
x
+
10
th
2
x
+
1
.
{\displaystyle \operatorname {th} 5x=\operatorname {th} x{\frac {\operatorname {th} ^{4}x+10\operatorname {th} ^{2}x+5}{5\operatorname {th} ^{4}x+10\operatorname {th} ^{2}x+1)).}
Произведения:
sh
x
sh
y
=
ch
(
x
+
y
)
−
ch
(
x
−
y
)
2
.
{\displaystyle \operatorname {sh} x\,\operatorname {sh} y={\frac {\operatorname {ch} (x+y)-\operatorname {ch} (x-y)}{2)).}
sh
x
ch
y
=
sh
(
x
+
y
)
+
sh
(
x
−
y
)
2
.
{\displaystyle \operatorname {sh} x\,\operatorname {ch} y={\frac {\operatorname {sh} (x+y)+\operatorname {sh} (x-y)}{2)).}
ch
x
ch
y
=
ch
(
x
+
y
)
+
ch
(
x
−
y
)
2
.
{\displaystyle \operatorname {ch} x\,\operatorname {ch} y={\frac {\operatorname {ch} (x+y)+\operatorname {ch} (x-y)}{2)).}
th
x
th
y
=
ch
(
x
+
y
)
−
ch
(
x
−
y
)
ch
(
x
+
y
)
+
ch
(
x
−
y
)
.
{\displaystyle \operatorname {th} x\,\operatorname {th} y={\frac {\operatorname {ch} (x+y)-\operatorname {ch} (x-y)}{\operatorname {ch} (x+y)+\operatorname {ch} (x-y))).}
Суммы:
sh
x
±
sh
y
=
2
sh
x
±
y
2
ch
x
∓
y
2
.
{\displaystyle \operatorname {sh} x\pm \operatorname {sh} y=2\operatorname {sh} {\frac {x\pm y}{2))\operatorname {ch} {\frac {x\mp y}{2)).}
ch
x
+
ch
y
=
2
ch
x
+
y
2
ch
x
−
y
2
.
{\displaystyle \operatorname {ch} x+\operatorname {ch} y=2\operatorname {ch} {\frac {x+y}{2))\operatorname {ch} {\frac {x-y}{2)).}
ch
x
−
ch
y
=
2
sh
x
+
y
2
sh
x
−
y
2
.
{\displaystyle \operatorname {ch} x-\operatorname {ch} y=2\operatorname {sh} {\frac {x+y}{2))\operatorname {sh} {\frac {x-y}{2)).}
th
x
±
th
y
=
sh
(
x
±
y
)
ch
x
ch
y
.
{\displaystyle \operatorname {th} x\pm \operatorname {th} y={\frac {\operatorname {sh} (x\pm y)}{\operatorname {ch} x\,\operatorname {ch} y)).}
Формулы понижения степени:
ch
2
x
2
=
ch
x
+
1
2
.
{\displaystyle \operatorname {ch} ^{2}{\frac {x}{2))={\frac {\operatorname {ch} x+1}{2)).}
sh
2
x
2
=
ch
x
−
1
2
.
{\displaystyle \operatorname {sh} ^{2}{\frac {x}{2))={\frac {\operatorname {ch} x-1}{2)).}
Разложение на множители:
2
(
1
+
ch
x
)
=
(
1
+
e
x
)
(
1
+
e
−
x
)
=
1
+
e
x
+
1
+
e
−
x
{\displaystyle 2(1+\operatorname {ch} x)=(1+{e^{x)))(1+{e^{-x)))=1+{e^{x))+1+{e^{-x))}
2
(
1
−
ch
x
)
=
(
1
−
e
x
)
(
1
−
e
−
x
)
=
1
−
e
x
+
1
−
e
−
x
{\displaystyle 2(1-\operatorname {ch} x)=(1-{e^{x)))(1-{e^{-x)))=1-{e^{x))+1-{e^{-x))}
Производные :Интегралы :
См. также: Список интегралов от гиперболических функций Список интегралов от обратных гиперболических функций
∫
sh
x
d
x
=
ch
x
+
C
.
{\displaystyle \int \operatorname {sh} x\,dx=\operatorname {ch} x+C.}
∫
ch
x
d
x
=
sh
x
+
C
.
{\displaystyle \int \operatorname {ch} x\,dx=\operatorname {sh} x+C.}
∫
th
x
d
x
=
ln
ch
x
+
C
.
{\displaystyle \int \operatorname {th} x\,dx=\ln \operatorname {ch} x+C.}
∫
1
ch
2
x
d
x
=
th
x
+
C
.
{\displaystyle \int {\frac {1}{\operatorname {ch} ^{2}x))\,dx=\operatorname {th} x+C.}
∫
1
sh
2
x
d
x
=
−
cth
x
+
C
.
{\displaystyle \int {\frac {1}{\operatorname {sh} ^{2}x))\,dx=-\operatorname {cth} x+C.}
sh
x
=
∫
0
x
ch
t
d
t
.
{\displaystyle \operatorname {sh} x=\int \limits _{0}^{x}\operatorname {ch} tdt.}
ch
x
=
1
+
∫
0
x
sh
t
d
t
.
{\displaystyle \operatorname {ch} x=1+\int \limits _{0}^{x}\operatorname {sh} tdt.}
th
x
=
∫
0
x
d
t
ch
2
t
.
{\displaystyle \operatorname {th} x=\int \limits _{0}^{x}{\frac {dt}{\operatorname {ch} ^{2}t)).}
Представление через гиперболический тангенс половинного угла :
sh
x
=
2
th
x
2
1
−
th
2
x
2
{\displaystyle \operatorname {sh} x={\frac {2\operatorname {th} {\frac {x}{2))}{1-\operatorname {th} ^{2}{\frac {x}{2))))}
ch
x
=
1
+
th
2
x
2
1
−
th
2
x
2
{\displaystyle \operatorname {ch} x={\frac {1+\operatorname {th} ^{2}{\frac {x}{2))}{1-\operatorname {th} ^{2}{\frac {x}{2))))}
th
x
=
2
th
x
2
1
+
th
2
x
2
{\displaystyle \operatorname {th} x={\frac {2\operatorname {th} {\frac {x}{2))}{1+\operatorname {th} ^{2}{\frac {x}{2))))}
cth
x
=
1
+
th
2
x
2
2
th
x
2
{\displaystyle \operatorname {cth} x={\frac {1+\operatorname {th} ^{2}{\frac {x}{2))}{2\operatorname {th} {\frac {x}{2))))}
sch
x
=
1
−
th
2
x
2
1
+
th
2
x
2
{\displaystyle \operatorname {sch} x={\frac {1-\operatorname {th} ^{2}{\frac {x}{2))}{1+\operatorname {th} ^{2}{\frac {x}{2))))}
csch
x
=
1
−
th
2
x
2
2
th
x
2
{\displaystyle \operatorname {csch} x={\frac {1-\operatorname {th} ^{2}{\frac {x}{2))}{2\operatorname {th} {\frac {x}{2))))}
Для всех
x
∈
R
{\displaystyle x\in \mathbb {R} }
0
≤
ch
x
−
1
≤
|
sh
x
|
<
ch
x
{\displaystyle 0\leq \operatorname {ch} x-1\leq |\operatorname {sh} x|<\operatorname {ch} x}
|
th
x
|
<
1
{\displaystyle |\operatorname {th} x|<1}
sh
x
=
x
+
x
3
3
!
+
x
5
5
!
+
x
7
7
!
+
…
=
∑
n
=
0
∞
x
2
n
+
1
(
2
n
+
1
)
!
{\displaystyle \operatorname {sh} \,x=x+{\frac {x^{3)){3!))+{\frac {x^{5)){5!))+{\frac {x^{7)){7!))+\ldots =\sum _{n=0}^{\infty }{\frac {x^{2n+1)){(2n+1)!))}
ch
x
=
1
+
x
2
2
!
+
x
4
4
!
+
x
6
6
!
+
…
=
∑
n
=
0
∞
x
2
n
(
2
n
)
!
{\displaystyle \operatorname {ch} \,x=1+{\frac {x^{2)){2!))+{\frac {x^{4)){4!))+{\frac {x^{6)){6!))+\ldots =\sum _{n=0}^{\infty }{\frac {x^{2n)){(2n)!))}
th
x
=
x
−
x
3
3
+
2
x
5
15
−
17
x
7
315
+
…
=
∑
n
=
1
∞
2
2
n
(
2
2
n
−
1
)
B
2
n
x
2
n
−
1
(
2
n
)
!
,
|
x
|
<
π
2
{\displaystyle \operatorname {th} \,x=x-{\frac {x^{3)){3))+{\frac {2x^{5)){15))-{\frac {17x^{7)){315))+\ldots =\sum _{n=1}^{\infty }{\frac {2^{2n}(2^{2n}-1)B_{2n}x^{2n-1)){(2n)!)),\quad |x|<{\frac {\pi }{2))}
cth
x
=
1
x
+
x
3
−
x
3
45
+
2
x
5
945
+
…
=
1
x
+
∑
n
=
1
∞
2
2
n
B
2
n
x
2
n
−
1
(
2
n
)
!
,
0
<
|
x
|
<
π
{\displaystyle \operatorname {cth} \,x={\frac {1}{x))+{\frac {x}{3))-{\frac {x^{3)){45))+{\frac {2x^{5)){945))+\ldots ={\frac {1}{x))+\sum _{n=1}^{\infty }{\frac {2^{2n}B_{2n}x^{2n-1)){(2n)!)),\quad 0<|x|<\pi }
Ряд Лорана )
sch
x
=
1
ch
x
=
∑
n
=
0
∞
E
2
n
x
2
n
(
2
n
)
!
{\displaystyle \operatorname {sch} \,x={\frac {1}{\operatorname {ch} \,x))=\sum _{n=0}^{\infty }{\frac {E_{2n}\,x^{2n)){(2n)!))}
Здесь
B
2
n
{\displaystyle B_{2n))
числа Бернулли ,
E
2
n
{\displaystyle E_{2n))
числа Эйлера .
sh(x) , ch(x) , th(x) , cth(x) sh , ch и th csch , sech и cth Гиперболический синус и гиперболический косинус аналитичны во всей комплексной плоскости, за исключением существенно особой точки на бесконечности. Гиперболический тангенс аналитичен везде, кроме полюсов в точках
z
=
i
π
(
n
+
1
/
2
)
{\displaystyle z=i\pi (n+1/2)}
n
{\displaystyle n}
Вычеты во всех этих полюсах равны единице. Гиперболический котангенс аналитичен везде, кроме точек
z
=
i
π
n
{\displaystyle z=i\pi n}
Иначе называются ареа-функциями: к названиям соответствующих гиперболических функций добавляется префикс «ареа-» — от лат. «area» — «площадь». Главные значения ареа-функций определяются следующими выражениями.
arsh
x
=
ln
(
x
+
x
2
+
1
)
{\displaystyle \operatorname {arsh} x=\ln(x+{\sqrt {x^{2}+1)))}
arch
x
=
ln
(
x
+
x
2
−
1
)
;
x
≥
1
{\displaystyle \operatorname {arch} x=\ln \left(x+{\sqrt {x^{2}-1))\right);x\geq 1}
arth
x
=
ln
1
−
x
2
1
−
x
=
1
2
ln
1
+
x
1
−
x
;
|
x
|
<
1
{\displaystyle \operatorname {arth} x=\ln {\frac {\sqrt {1-x^{2))}{1-x))={\frac {1}{2))\ln {\frac {1+x}{1-x));|x|<1}
arcth
x
=
ln
x
2
−
1
x
−
1
=
1
2
ln
x
+
1
x
−
1
;
|
x
|
>
1
{\displaystyle \operatorname {arcth} x=\ln {\frac {\sqrt {x^{2}-1)){x-1))={\frac {1}{2))\ln {\frac {x+1}{x-1));|x|>1}
arsch
x
=
ln
1
+
1
−
x
2
x
;
0
<
x
≤
1
{\displaystyle \operatorname {arsch} x=\ln {\frac {1+{\sqrt {1-x^{2)))){x));0<x\leq 1}
y
=
−
ln
1
+
1
−
x
2
x
{\displaystyle y=-\ln {\frac {1+{\sqrt {1-x^{2)))){x))}
sch
y
=
x
{\displaystyle \operatorname {sch} y=x}
arcsch
x
=
ln
1
+
sgn
x
1
+
x
2
x
=
{
ln
1
−
1
+
x
2
x
,
x
<
0
ln
1
+
1
+
x
2
x
,
x
>
0
{\displaystyle \operatorname {arcsch} x=\ln {\frac {1+\operatorname {sgn} x{\sqrt {1+x^{2)))){x))=\left\((\begin{array}{l}\ln {\frac {1-{\sqrt {1+x^{2)))){x)),\quad x<0\\\ln {\frac {1+{\sqrt {1+x^{2)))){x)),\quad x>0\end{array))\right.}
arsh(x) , arch(x) , arth(x) , arcth(x) Связь между некоторыми обратными гиперболическими и обратными тригонометрическими функциями:
Arsh
x
=
−
i
Arcsin
(
−
i
x
)
,
{\displaystyle \operatorname {Arsh} x=-i\operatorname {Arcsin} (-ix),}
Arsh
(
i
x
)
=
i
Arcsin
x
,
{\displaystyle \operatorname {Arsh} (ix)=i\operatorname {Arcsin} x,}
Arcsin
x
=
−
i
Arsh
(
i
x
)
,
{\displaystyle \operatorname {Arcsin} x=-i\operatorname {Arsh} (ix),}
Arcsin
(
i
x
)
=
−
i
Arsh
(
−
x
)
,
{\displaystyle \operatorname {Arcsin} (ix)=-i\operatorname {Arsh} (-x),}
Arccos
x
=
−
i
Arch
x
,
{\displaystyle \operatorname {Arccos} \ x=-i\ \operatorname {Arch} \ x,}
где i — мнимая единица .
Эти функции имеют следующее разложение в ряд:
arsh
x
=
x
−
(
1
2
)
x
3
3
+
(
1
⋅
3
2
⋅
4
)
x
5
5
−
(
1
⋅
3
⋅
5
2
⋅
4
⋅
6
)
x
7
7
+
…
=
∑
n
=
0
∞
(
(
−
1
)
n
(
2
n
)
!
2
2
n
(
n
!
)
2
)
x
2
n
+
1
2
n
+
1
,
|
x
|
<
1
;
{\displaystyle \operatorname {arsh} x=x-\left({\frac {1}{2))\right){\frac {x^{3)){3))+\left({\frac {1\cdot 3}{2\cdot 4))\right){\frac {x^{5)){5))-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6))\right){\frac {x^{7)){7))+\ldots =\sum _{n=0}^{\infty }\left({\frac {(-1)^{n}(2n)!}{2^{2n}(n!)^{2))}\right){\frac {x^{2n+1)){2n+1)),\quad \left\vert x\right\vert <1;}
arch
x
=
ln
(
2
x
)
−
(
(
1
2
)
x
−
2
2
+
(
1
⋅
3
2
⋅
4
)
x
−
4
4
+
(
1
⋅
3
⋅
5
2
⋅
4
⋅
6
)
x
−
6
6
+
…
)
=
ln
(
2
x
)
−
∑
n
=
1
∞
(
(
−
1
)
n
(
2
n
)
!
2
2
n
(
n
!
)
2
)
x
−
2
n
2
n
,
x
>
1
;
{\displaystyle \operatorname {arch} x=\ln(2x)-\left(\left({\frac {1}{2))\right){\frac {x^{-2)){2))+\left({\frac {1\cdot 3}{2\cdot 4))\right){\frac {x^{-4)){4))+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6))\right){\frac {x^{-6)){6))+\ldots \right)=\ln(2x)-\sum _{n=1}^{\infty }\left({\frac {(-1)^{n}(2n)!}{2^{2n}(n!)^{2))}\right){\frac {x^{-2n)){2n)),\quad x>1;}
arth
x
=
x
+
x
3
3
+
x
5
5
+
x
7
7
+
…
=
∑
n
=
0
∞
x
2
n
+
1
2
n
+
1
,
|
x
|
<
1.
{\displaystyle \operatorname {arth} x=x+{\frac {x^{3)){3))+{\frac {x^{5)){5))+{\frac {x^{7)){7))+\ldots =\sum _{n=0}^{\infty }{\frac {x^{2n+1)){2n+1)),\quad |x|<1.}
В зарубежной литературе обратные гиперболические функции часто обозначают посредством знака минус первой степени: например,
Arth
x
{\displaystyle \operatorname {Arth} \,x}
tanh
−
1
x
{\displaystyle \operatorname {tanh} ^{-1}x}
(
tanh
x
)
−
1
{\displaystyle (\operatorname {tanh} \,x)^{-1))
cth
x
{\displaystyle \operatorname {cth} \,x}
Первое появление гиперболических функций историки обнаружили в трудах английского математика Абрахама де Муавра (1707 , 1722 ). Современное определение и обстоятельное их исследование выполнил Винченцо Риккати в 1757 году («Opusculorum», том I), он же предложил их обозначения:
sh
{\displaystyle \operatorname {sh} }
ch
{\displaystyle \operatorname {ch} }
#Определение ).
Независимое открытие и дальнейшее исследование свойств гиперболических функций было проведено Иоганном Ламбертом (1768 ), который установил широкий параллелизм формул обычной и гиперболической тригонометрии. Н. И. Лобачевский впоследствии использовал этот параллелизм, пытаясь доказать непротиворечивость неевклидовой геометрии , в которой круговая тригонометрия заменяется на гиперболическую.
В обозначениях гиперболических функций утвердился некоторый разнобой. Например, в Энциклопедии Брокгауза и Эфрона используются обозначения
sinhyp
{\displaystyle \operatorname {sinhyp} }
coshyp
{\displaystyle \operatorname {coshyp} }
sh
,
ch
{\displaystyle \operatorname {sh} ,\operatorname {ch} }
sinh
,
cosh
{\displaystyle \sinh ,\cosh }
Гиперболические функции часто встречаются при вычислении различных интегралов . Некоторые интегралы от рациональных функций и от функций, содержащих радикалы, довольно просто вычисляются с помощью замен переменных с использованием гиперболических функций.
Аналогично тому, как матрицы вида
(
cos
x
sin
x
−
sin
x
cos
x
)
{\displaystyle {\begin{pmatrix}\cos x&\sin x\\-\sin x&\cos x\end{pmatrix))}
евклидова пространства , матрицы
(
c
h
x
s
h
x
s
h
x
c
h
x
)
{\displaystyle {\begin{pmatrix}\mathop {\mathrm {ch} } \,x&\mathop {\mathrm {sh} } \,x\\\mathop {\mathrm {sh} } \,x&\mathop {\mathrm {ch} } \,x\end{pmatrix))}
пространстве Минковского . В связи с этим гиперболические функции часто встречаются в теории относительности .
Однородная бесконечно гибкая веревка или цепочка, свободно подвешенная за свои концы, приобретает форму графика функции
y
=
a
c
h
x
a
{\displaystyle y=a\,\mathop {\mathrm {ch} } \,{\frac {x}{a))}
цепной линией арок , поскольку форма арки в виде перевёрнутой цепной линии наиболее эффективно распределяет нагрузку.
Бугров Я. С., Никольский С. М. Высшая математика. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. — Москва: Наука, 1985. — С. 464.Шерватов В. Г. Гиперболические функции.. — Гостехиздат, 1954. — 58 с. — (Популярные лекции по математике ). — 25 000 экз. А. Р. Янпольский. Гиперболические функции. — Москва, 1960. — 195 с.Для улучшения этой статьи
желательно :
Проставить
сноски , внести более точные указания на источники.После исправления проблемы исключите её из списка. Удалите шаблон, если устранены все недостатки.
Ссылки на внешние ресурсы
Словари и энциклопедии В библиографических каталогах