A számelméletben a téglalapszámok olyan figurális számok, melyek felírhatók két, egymást követő nemnegatív egész szám szorzataként, tehát n(n + 1) alakban.^[1] Már Arisztotelész is tanulmányozta őket. A téglalapszámok általánosíthatók az n(n + k) alakú számokra.

Az első néhány téglalapszám:

0, 2, 6, 12, 20, 30, 42, 56, 72, 90, 110, 132, 156, 182, 210, 240, 272, 306, 342, 380, 420, 462 … (A002378 sorozat az OEIS-ben).

Arisztotelész metafizikájában a téglalapszámokat más figurális számokkal, a háromszögszámokkal és négyzetszámokkal együtt tanulmányozták,^[2] felfedezésük még korábbra, a püthagoreusokhoz köthető.^[3] A sokszögszámok mintájára:

1×2	2×3	3×4	4×5

Az n-edik téglalapszám épp kétszerese az n-edik háromszögszámnak^[1][2] és n-nel haladja meg az n-edik négyzetszámot, ami az alternatív n² + n képletükből is világos. Az n-edik téglalapszám éppen a páratlan négyzetszám (2n + 1)² és az (n+1)-edik középpontos hatszögszám közötti különbség.

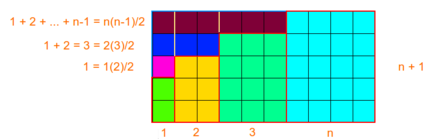
A téglalapszámok figurális mivoltuk miatt a legegyszerűbben téglalapokként ábrázolhatóak, ahogyan az ábrán látható. Az első n téglalapszám összegét meghatározhatjuk, ha a nagy téglalap területéből kivonjuk a nem kellő területeket.

A nagy téglalap területe ${\displaystyle (1+2+\cdots +n)\cdot (n+1)={\frac {n(n+1)^{2)){2))}$.

Megfigyelhető, hogy a felesleges részek területei soronként az első 1, 2, ..., n-1 pozitív szám összegei, azaz ${\displaystyle (1)+(1+2)+\cdots +(1+2+\cdots +n-1)={\frac {1(2)}{2))+{\frac {2(3)}{2))+\cdots +{\frac {n(n-1)}{2))}$.

Továbbá látható, hogy a felesleges részek pontosan az első n-1 téglalapszám összegének a fele.

Ekkor ha ${\displaystyle f(n)}$ az első n téglalapszám összegét adja meg, akkor ${\displaystyle f(n)={\frac {n(n+1)^{2)){2))-{\frac {f(n-1)}{2))}$.

Felhasználva, hogy ${\displaystyle f(n)=f(n-1)+n(n+1)}$ és az algebra szabályait segítségül hívva:

${\displaystyle f(n)={\frac {n(n+1)^{2}-f(n)+n(n+1)}{2))}$

${\displaystyle 2f(n)=n(n+1)^{2}-f(n)+n(n+1)}$

${\displaystyle 3f(n)=n(n+1)^{2}+n(n+1)}$

${\displaystyle 3f(n)=n(n+1)(n+1+1)}$

${\displaystyle f(n)={\frac {n(n+1)(n+2)}{3))}$

Azaz

${\displaystyle \sum _{i=1}^{n}i(i+1)={\frac {n(n+1)(n+2)}{3))}$

Az első n pozitív téglalapszám reciprokösszege a következőképpen alakul:

${\displaystyle {\frac {1}{1\cdot 2))+{\frac {1}{2\cdot 3))+{\frac {1}{3\cdot 4))+\cdots +{\frac {1}{(n-1)\cdot n))+{\frac {1}{n\cdot (n+1)))}$

${\displaystyle =\left({\frac {1}{1))-{\frac {1}{2))\right)+\left({\frac {1}{2))-{\frac {1}{3))\right)+\cdots +\left({\frac {1}{n-1))-{\frac {1}{n))\right)+\left({\frac {1}{n))-{\frac {1}{n+1))\right)}$

${\displaystyle ={\frac {1}{1))+\left(-{\frac {1}{2))+{\frac {1}{2))\right)+\left(-{\frac {1}{3))+{\frac {1}{3))\right)+\cdots +\left(-{\frac {1}{n-1))+{\frac {1}{n-1))\right)+\left(-{\frac {1}{n))+{\frac {1}{n))\right)-{\frac {1}{n+1))}$

${\displaystyle =1-{\frac {1}{n+1))}$

${\displaystyle ={\frac {n}{n+1))}$

Ebből kifolyólag a pozitív téglalapszámok reciprokösszege 1:^[4]

${\displaystyle \sum _{i=1}^{\infty }{\frac {1}{i(i+1)))=\lim _{n\rightarrow \infty }{\frac {n}{n+1))=1}$

A téglalapszámok általánosíthatóak ${\displaystyle n(n+k)}$ alakúra, ahol ${\displaystyle k\in \mathbb {Z} ^{+))$. Ebben az esetben az első n pozitív téglalapszám reciprokösszege a következő:

${\displaystyle {\frac {1}{1\cdot (1+k)))+{\frac {1}{2\cdot (2+k)))+{\frac {1}{3\cdot (3+k)))+\cdots +{\frac {1}{(n-1)\cdot (n+k-1)))+{\frac {1}{n\cdot (n+k)))}$

${\displaystyle ={\frac {1}{k))\cdot {\Biggr [}\left({\frac {1}{1))-{\frac {1}{1+k))\right)+\left({\frac {1}{2))-{\frac {1}{2+k))\right)+\cdots +\left({\frac {1}{n-1))-{\frac {1}{n+k-1))\right)+\left({\frac {1}{n))-{\frac {1}{n+k))\right){\Biggr ]))$

${\displaystyle ={\frac {1}{k))\cdot {\Biggr [}\left({\frac {1}{1))+{\frac {1}{2))+\cdots +{\frac {1}{n))\right)+\left(-{\frac {1}{1+k))-{\frac {1}{2+k))-\cdots -{\frac {1}{n+k))\right){\Biggr ]))$

${\displaystyle ={\frac {1}{k))\cdot {\Biggr [}H_{n}-\left(H_{n+k}-H_{k}\right){\Biggr ]}={\frac {1}{k))\cdot {\Biggr [}H_{k}+H_{n}-H_{n+k}{\Biggr ]))$

ahol a ${\displaystyle H_{n))$ az első n pozitív egész szám reciprokainak összegét, azaz az n-dik harmonikus számot adja meg.

Ezen összeg ${\displaystyle n\rightarrow \infty }$ esetben:

${\displaystyle \sum _{i=1}^{\infty }{\frac {1}{i(i+k)))=\lim _{n\rightarrow \infty }{\frac {1}{k))\cdot {\Biggr [}H_{k}+H_{n}-H_{n+k}{\Biggr ]}={\frac {1}{k))\cdot {\Biggr [}\lim _{n\rightarrow \infty }H_{k}+\lim _{n\rightarrow \infty }\left(H_{n}-H_{n+k}\right){\Biggr ]}={\frac {H_{k)){k))}$

Következtetésképpen megállapíthatjuk, hogy a k különbségű pozitív téglalapszámok reciprokainak összege ${\displaystyle {\frac {H_{k)){k))}$, ahol ${\displaystyle H_{k))$ a k-dik harmonikus szám.

Az n-edik téglalapszám megegyezik az első n páros egész szám összegével.^[2] Ebből következik az is, hogy az összes téglalapszám páros, és közülük egyedül a 2 prímszám. Szintén a 2 az egyetlen Fibonacci-téglalapszám és az egyetlen téglalap Lucas-szám.^[5][6]

A négyzetes mátrix átlón kívüli elemeinek száma mindig téglalapszám.^[7]

A tény, hogy az egymást követő egészek mindig relatív prímek, a téglalapszámok pedig két egymást követő egész szorzatai, néhány új tulajdonsághoz vezetnek. A téglalapszám minden prímtényezője az őt alkotó tényezők közül pontosan az egyikben fordul elő. Tehát egy téglalapszám csakkor négyzetmentes, ha n és n + 1 is négyzetmentesek. A téglalapszámok különböző prímtényezőinek száma megegyezik az n és n + 1 különböző prímtényezői számának összegével.

További tulajdonsága a téglalapszámoknak, hogy az n-nél 0,5-del nagyobb szám négyzete pont az n-edik téglalapszámnál 0,25-dal nagyobb. Például: 7,5² = 56,25. Ezért az 5-re végződő egész négyzetszámok négyzete 25-re végződik úgy, hogy az azt megelőző számjegyek téglalapszámot alkotnak.

Még egy másik tulajdonságuk, hogy bármelyik n alapú számrendszerben az n-edik, vagyis a számrendszer alapszámával megegyező sorszámú téglalapszám 110 alakban írható fel. Például a nyolcas számrendszerben az 110₈ szám 72-t jelent, amely pont a 8. téglalapszám. A tízes számrendszerben épp a tizedik téglalapszám írható fel 110 (száztíz) alakban. Ennek oka ugyanaz, ami miatt a n² + n is az egyik kiszámítási képlet alternatívája, vagyis az n-edik téglalapszám az n szám (számrendszer alapszáma) első két hatványának összege.

• Tuzson Zoltán: A figurális számokról (II)

• Ez a szócikk részben vagy egészben a Pronic number című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

Sablon:Osztóosztályok m v sz Az egész számok oszthatóságon alapuló csoportosítása
Áttekintés	Prímfelbontás Osztó Unitary divisor Osztószám-függvény Osztóösszeg-függvényregul Prímtényező A számelmélet alaptétele Aritmetikus számok
Prímtényezős felbontás	Prím Összetett Félprím Téglalapszám Szfenikus Négyzetmentes Hatványteljes Teljes hatvány Achilles Sima Szabályos Durva Szokásos/szokatlan
Osztóösszegek	Tökéletes Majdnem tökéletes Kvázitökéletes Többszörösen tökéletes Féltökéletes Hipertökéletes Szupertökéletes Unitary perfect Áltökéletes Praktikus Erdős–Nicolas
Sok osztóval rendelkező	Bővelkedő Primitív bővelkedő Erősen bővelkedő Szuperbővelkedő Kolosszálisan bővelkedő Erősen összetett Kiváló erősen összetett Furcsa
Osztóösszeg-sorozattal kapcsolatos	Érinthetetlen Erősen érinthető Barátságos Társas Eljegyzett
Egyéb csoportok	Hiányos Friendly Solitary Sublime Osztóharmonikus Frugal Equidigital Extravagáns