Algebraic structure → Group theory Group theory
Basic notions Subgroup Normal subgroup Quotient group (Semi-)direct product Group homomorphisms kernel image direct sum wreath product simple finite infinite continuous multiplicative additive cyclic abelian dihedral nilpotent solvable action Glossary of group theory List of group theory topics
Finite groups Cyclic group Zn Symmetric group Sn Alternating group An Dihedral group Dn Quaternion group Q Cauchy's theorem Lagrange's theorem Sylow theorems Hall's theorem p-group Elementary abelian group Frobenius group Schur multiplier Classification of finite simple groups cyclic alternating Lie type sporadic
Discrete groups Lattices Integers (${\displaystyle \mathbb {Z} }$) Free group Modular groups PSL(2, ${\displaystyle \mathbb {Z} }$) SL(2, ${\displaystyle \mathbb {Z} }$) Arithmetic group Lattice Hyperbolic group
Topological and Lie groups Solenoid Circle General linear GL(n) Special linear SL(n) Orthogonal O(n) Euclidean E(n) Special orthogonal SO(n) Unitary U(n) Special unitary SU(n) Symplectic Sp(n) G2 F4 E6 E7 E8 Lorentz Poincaré Conformal Diffeomorphism Loop Infinite dimensional Lie group O(∞) SU(∞) Sp(∞)
Algebraic groups Linear algebraic group Reductive group Abelian variety Elliptic curve
v t e

In mathematics, given two groups, (G,∗) and (H, ·), a group homomorphism from (G,∗) to (H, ·) is a function h : G → H such that for all u and v in G it holds that

${\displaystyle h(u*v)=h(u)\cdot h(v)}$

where the group operation on the left side of the equation is that of G and on the right side that of H.

From this property, one can deduce that h maps the identity element e_G of G to the identity element e_H of H,

${\displaystyle h(e_{G})=e_{H))$

and it also maps inverses to inverses in the sense that

${\displaystyle h\left(u^{-1}\right)=h(u)^{-1}.\,}$

Hence one can say that h "is compatible with the group structure".

In areas of mathematics where one considers groups endowed with additional structure, a homomorphism sometimes means a map which respects not only the group structure (as above) but also the extra structure. For example, a homomorphism of topological groups is often required to be continuous.

Intuition

The purpose of defining a group homomorphism is to create functions that preserve the algebraic structure. An equivalent definition of group homomorphism is: The function h : G → H is a group homomorphism if whenever

a ∗ b = c   we have   h(a) ⋅ h(b) = h(c).

In other words, the group H in some sense has a similar algebraic structure as G and the homomorphism h preserves that.

Types

Monomorphism

A group homomorphism that is injective (or, one-to-one); i.e., preserves distinctness.

Epimorphism

A group homomorphism that is surjective (or, onto); i.e., reaches every point in the codomain.

Isomorphism

A group homomorphism that is bijective; i.e., injective and surjective. Its inverse is also a group homomorphism. In this case, the groups G and H are called isomorphic; they differ only in the notation of their elements (except of identity element) and are identical for all practical purposes. I.e. we re-label all elements except identity.

Endomorphism

A group homomorphism, h: G → G; the domain and codomain are the same. Also called an endomorphism of G.

Automorphism

A group endomorphism that is bijective, and hence an isomorphism. The set of all automorphisms of a group G, with functional composition as operation, itself forms a group, the automorphism group of G. It is denoted by Aut(G). As an example, the automorphism group of (Z, +) contains only two elements, the identity transformation and multiplication with −1; it is isomorphic to (Z/2Z, +).

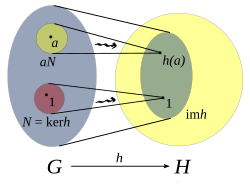
Image and kernel

We define the kernel of h to be the set of elements in G which are mapped to the identity in H

${\displaystyle \operatorname {ker} (h):=\left\{u\in G\colon h(u)=e_{H}\right\}.}$

and the image of h to be

${\displaystyle \operatorname {im} (h):=h(G)\equiv \left\{h(u)\colon u\in G\right\}.}$

The kernel and image of a homomorphism can be interpreted as measuring how close it is to being an isomorphism. The first isomorphism theorem states that the image of a group homomorphism, h(G) is isomorphic to the quotient group G/ker h.

The kernel of h is a normal subgroup of G:

${\displaystyle {\begin{aligned}h\left(g^{-1}\circ u\circ g\right)&=h(g)^{-1}\cdot h(u)\cdot h(g)\\&=h(g)^{-1}\cdot e_{H}\cdot h(g)\\&=h(g)^{-1}\cdot h(g)=e_{H},\end{aligned))}$

and the image of h is a subgroup of H.

The homomorphism, h, is a group monomorphism; i.e., h is injective (one-to-one) if and only if ker(h) = {e_G}. Injection directly gives that there is a unique element in the kernel, and, conversely, a unique element in the kernel gives injection:

${\displaystyle {\begin{aligned}&&h(g_{1})&=h(g_{2})\\\Leftrightarrow &&h(g_{1})\cdot h(g_{2})^{-1}&=e_{H}\\\Leftrightarrow &&h\left(g_{1}\circ g_{2}^{-1}\right)&=e_{H},\ \operatorname {ker} (h)=\{e_{G}\}\\\Rightarrow &&g_{1}\circ g_{2}^{-1}&=e_{G}\\\Leftrightarrow &&g_{1}&=g_{2}\end{aligned))}$

Examples

• Consider the cyclic group Z₃ = (Z/3Z, +) = ({0, 1, 2}, +) and the group of integers (Z, +). The map h : Z → Z/3Z with h(u) = u mod 3 is a group homomorphism. It is surjective and its kernel consists of all integers which are divisible by 3.

• The exponential map yields a group homomorphism from the group of real numbers R with addition to the group of non-zero real numbers R* with multiplication. The kernel is {0} and the image consists of the positive real numbers.
• The exponential map also yields a group homomorphism from the group of complex numbers C with addition to the group of non-zero complex numbers C* with multiplication. This map is surjective and has the kernel {2πki : k ∈ Z}, as can be seen from Euler's formula. Fields like R and C that have homomorphisms from their additive group to their multiplicative group are thus called exponential fields.
• The function ${\displaystyle \Phi :(\mathbb {N} ,+)\rightarrow (\mathbb {R} ,+)}$, defined by ${\displaystyle \Phi (x)={\sqrt[{}]{2))x}$ is a homomorphism.
• Consider the two groups ${\displaystyle (\mathbb {R} ^{+},*)}$ and ${\displaystyle (\mathbb {R} ,+)}$, represented respectively by ${\displaystyle G}$ and ${\displaystyle H}$, where ${\displaystyle \mathbb {R} ^{+))$ is the positive real numbers. Then, the function ${\displaystyle f:G\rightarrow H}$ defined by the logarithm function is a homomorphism.

Category of groups

If h : G → H and k : H → K are group homomorphisms, then so is k ∘ h : G → K. This shows that the class of all groups, together with group homomorphisms as morphisms, forms a category.

Homomorphisms of abelian groups

If G and H are abelian (i.e., commutative) groups, then the set Hom(G, H) of all group homomorphisms from G to H is itself an abelian group: the sum h + k of two homomorphisms is defined by

(h + k)(u) = h(u) + k(u)    for all u in G.

The commutativity of H is needed to prove that h + k is again a group homomorphism.

The addition of homomorphisms is compatible with the composition of homomorphisms in the following sense: if f is in Hom(K, G), h, k are elements of Hom(G, H), and g is in Hom(H, L), then

(h + k) ∘ f = (h ∘ f) + (k ∘ f)    and    g ∘ (h + k) = (g ∘ h) + (g ∘ k).

Since the composition is associative, this shows that the set End(G) of all endomorphisms of an abelian group forms a ring, the endomorphism ring of G. For example, the endomorphism ring of the abelian group consisting of the direct sum of m copies of Z/nZ is isomorphic to the ring of m-by-m matrices with entries in Z/nZ. The above compatibility also shows that the category of all abelian groups with group homomorphisms forms a preadditive category; the existence of direct sums and well-behaved kernels makes this category the prototypical example of an abelian category.