In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of injective module. This concept is important in cohomology, in homotopy theory and in the theory of model categories. The dual notion is that of a projective object.

An object ${\displaystyle Q}$ in a category ${\displaystyle \mathbf {C} }$ is said to be injective if for every monomorphism ${\displaystyle f:X\to Y}$ and every morphism ${\displaystyle g:X\to Q}$ there exists a morphism ${\displaystyle h:Y\to Q}$ extending ${\displaystyle g}$ to ${\displaystyle Y}$, i.e. such that ${\displaystyle h\circ f=g}$.^[1]

That is, every morphism ${\displaystyle X\to Q}$ factors through every monomorphism ${\displaystyle X\hookrightarrow Y}$.

The morphism ${\displaystyle h}$ in the above definition is not required to be uniquely determined by ${\displaystyle f}$ and ${\displaystyle g}$.

In a locally small category, it is equivalent to require that the hom functor ${\displaystyle \operatorname {Hom} _{\mathbf {C} }(-,Q)}$ carries monomorphisms in ${\displaystyle \mathbf {C} }$ to surjective set maps.

The notion of injectivity was first formulated for abelian categories, and this is still one of its primary areas of application. When ${\displaystyle \mathbf {C} }$ is an abelian category, an object Q of ${\displaystyle \mathbf {C} }$ is injective if and only if its hom functor Hom_C(–,Q) is exact.

If ${\displaystyle 0\to Q\to U\to V\to 0}$ is an exact sequence in ${\displaystyle \mathbf {C} }$ such that Q is injective, then the sequence splits.

The category ${\displaystyle \mathbf {C} }$ is said to have enough injectives if for every object X of ${\displaystyle \mathbf {C} }$, there exists a monomorphism from X to an injective object.

A monomorphism g in ${\displaystyle \mathbf {C} }$ is called an essential monomorphism if for any morphism f, the composite fg is a monomorphism only if f is a monomorphism.

If g is an essential monomorphism with domain X and an injective codomain G, then G is called an injective hull of X. The injective hull is then uniquely determined by X up to a non-canonical isomorphism.^[1]

• In the category of abelian groups and group homomorphisms, Ab, an injective object is necessarily a divisible group. Assuming the axiom of choice, the notions are equivalent.
• In the category of (left) modules and module homomorphisms, R-Mod, an injective object is an injective module. R-Mod has injective hulls (as a consequence, R-Mod has enough injectives).
• In the category of metric spaces, Met, an injective object is an injective metric space, and the injective hull of a metric space is its tight span.
• In the category of T₀ spaces and continuous mappings, an injective object is always a Scott topology on a continuous lattice, and therefore it is always sober and locally compact.

If an abelian category has enough injectives, we can form injective resolutions, i.e. for a given object X we can form a long exact sequence

${\displaystyle 0\to X\to Q^{0}\to Q^{1}\to Q^{2}\to \cdots }$

and one can then define the derived functors of a given functor F by applying F to this sequence and computing the homology of the resulting (not necessarily exact) sequence. This approach is used to define Ext, and Tor functors and also the various cohomology theories in group theory, algebraic topology and algebraic geometry. The categories being used are typically functor categories or categories of sheaves of O_X modules over some ringed space (X, O_X) or, more generally, any Grothendieck category.

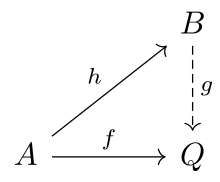
Let ${\displaystyle \mathbf {C} }$ be a category and let ${\displaystyle {\mathcal {H))}$ be a class of morphisms of ${\displaystyle \mathbf {C} }$.

An object ${\displaystyle Q}$ of ${\displaystyle \mathbf {C} }$ is said to be ${\displaystyle {\mathcal {H))}$-injective if for every morphism ${\displaystyle f:A\to Q}$ and every morphism ${\displaystyle h:A\to B}$ in ${\displaystyle {\mathcal {H))}$ there exists a morphism ${\displaystyle g:B\to Q}$ with ${\displaystyle g\circ h=f}$.

If ${\displaystyle {\mathcal {H))}$ is the class of monomorphisms, we are back to the injective objects that were treated above.

The category ${\displaystyle \mathbf {C} }$ is said to have enough ${\displaystyle {\mathcal {H))}$-injectives if for every object X of ${\displaystyle \mathbf {C} }$, there exists an ${\displaystyle {\mathcal {H))}$-morphism from X to an ${\displaystyle {\mathcal {H))}$-injective object.

A ${\displaystyle {\mathcal {H))}$-morphism g in ${\displaystyle \mathbf {C} }$ is called ${\displaystyle {\mathcal {H))}$-essential if for any morphism f, the composite fg is in ${\displaystyle {\mathcal {H))}$ only if f is in ${\displaystyle {\mathcal {H))}$.

If g is a ${\displaystyle {\mathcal {H))}$-essential morphism with domain X and an ${\displaystyle {\mathcal {H))}$-injective codomain G, then G is called an ${\displaystyle {\mathcal {H))}$-injective hull of X.^[1]

• In the category of simplicial sets, the injective objects with respect to the class ${\displaystyle {\mathcal {H))}$ of anodyne extensions are Kan complexes.
• In the category of partially ordered sets and monotone maps, the complete lattices form the injective objects for the class ${\displaystyle {\mathcal {H))}$ of order-embeddings, and the Dedekind–MacNeille completion of a partially ordered set is its ${\displaystyle {\mathcal {H))}$-injective hull.

• Projective object

• Jiri Adamek, Horst Herrlich, George Strecker. Abstract and concrete categories: The joy of cats, Chapter 9, Injective Objects and Essential Embeddings, Republished in Reprints and Applications of Categories, No. 17 (2006) pp. 1-507, Wiley (1990).
• J. Rosicky, Injectivity and accessible categories
• F. Cagliari and S. Montovani, T₀-reflection and injective hulls of fibre spaces