Лема про змію — інструмент, який використовується в математиці, особливо в гомологічній алгебрі, для побудови довгих точних послідовностей. Лема про змію є вірною в будь-якій абелевій категорії і відіграє ключову роль в гомологічній алгебрі і її застосуваннях, наприклад в алгебраїчної топології. Гомоморфізми, побудовані з її допомогою, зазвичай називають зв'язуючими гомоморфізмами.

У абелевій категорії (такий як категорія абелевих груп або категорія векторних просторів над фіксованим полем), розглянемо комутативну діаграму:

рядки якої є точними послідовностями, а 0 — нульовий об'єкт.

Тоді існує точна послідовність, що зв'язує ядра і коядра відображень a, b і c:

${\displaystyle \ker a~{\color {Gray}\longrightarrow }~\ker b~{\color {Gray}\longrightarrow }~\ker c~{\overset {d}{\longrightarrow ))~\operatorname {coker} a~{\color {Gray}\longrightarrow }~\operatorname {coker} b~{\color {Gray}\longrightarrow }~\operatorname {coker} c}$

де d — гомоморфізм, що називається зв'язуючим гомоморфізмом.

Більш того, якщо морфізм f є мономорфізмом, то і морфізм ${\displaystyle \operatorname {ker} a~{\color {Gray}\longrightarrow }~\operatorname {ker} b}$ — мономорфізм, і якщо g' є епіморфізмом, то і ${\displaystyle \operatorname {coker} b~{\color {Gray}\longrightarrow }~\operatorname {coker} c}$ — епіморфізм.

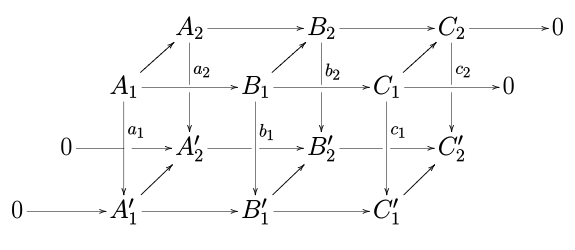
Щоб пояснити походження назви леми, уявімо наведену вище діаграму наступним чином:

і зауважимо, що точна послідовність, існування якої стверджується у лемі, має форму повзучої змії.

Відображення між ядрами і відображення між коядрами природним чином індукуються даними (горизонтальними) відображеннями зважаючи на комутативність діаграми. Точність двох індукованих послідовностей природним чином випливає з точності рядків вихідної діаграми. Важлива частина твердження леми полягає в існуванні зв'язуючого гомоморфізму d, що включається в точну послідовність.

У випадку абелевих груп або модулів над деякими кільцем, відображення d може бути побудовано в такий спосіб:

Виберемо елемент x з ker c і розглянемо його як елемент C; так як g є сюр'єктивним, то існує y з B, такий, що g(y) = x. З огляду на комутативність діаграми, ми маємо g' (b(y)) =c(g(y)) =c(x) = 0 (так як x лежить в ядрі c), і отже b(y) лежить в ядрі g' . Так як нижній рядок є точним, то існує елемент z з A' , такий, що f' (z) = b(y). Елемент z є єдиним зважаючи на ін'єктивність f' . Тоді можна задати d(x) = z + im(a). Залишається перевірити, що d є коректно визначеним (тобто d(x) залежить тільки від x, а не від вибору y), що він є гомоморфізмом і що одержана послідовність є точною.

Якщо це зробити, теорема буде доведена для абелевих груп або для модулів над кільцем. У загальному випадку доведення можна переформулювати в термінах властивостей стрілок. Інший спосіб ведення — використання теореми Мітчела про вкладення.

В застосуваннях, часто потрібно довести, що отримана довга точна послідовність є "натуральною" (в розумінні натуральних перетворень). Ці властивості випливають із натуральності послідовності у лемі про змію.

А саме, якщо маємо комутативну діаграму

в якій усі рядки є точними, то лему про змію можна застосувати для "передньої" і "задньої частин діаграм", отримавши дві довгі точні послідовності. Ці точні послідовності пов'язані комутативною діаграмою

Нехай дано точну послідовність ланцюгових комплексів:

${\displaystyle 0\;{\xrightarrow {))\;K\;{\xrightarrow {F))\;L\;{\xrightarrow {G))\;M\;{\xrightarrow {))\;0}$

із гомоморфізмами ланцюгових комплексів ${\displaystyle F,G.}$

Точність послідовності в даному випадку означає, що усі відповідні послідовності модулів

${\displaystyle 0\;{\xrightarrow {))\;K_{n}\;{\xrightarrow {F_{n))}\;L_{n}\;{\xrightarrow {G_{n))}\;M_{n}\;{\xrightarrow {))\;0}$

є точними.

Одним із найважливіших наслідків леми про змію, що широко використовується у гомологічній алгебрі і алгебричній топології є твердження про те, що за таких умов існують гомоморфізми ${\displaystyle \partial _{n}:H_{n}(M)\to H_{n-1}(K),}$які є частиною довгої точної послідовності:

${\displaystyle \ldots {\xrightarrow {))\;H_{n}(K)\;{\xrightarrow {F_{n))}\;H_{n}(L)\;{\xrightarrow {G_{n))}\;H_{n}(M)\;{\xrightarrow {\partial _{n))}H_{n-1}(K)\;{\xrightarrow {))\ldots }$

Зважаючи на умови точності послідовності ланцюгових комплексів, одержується комутативна діаграма:

${\displaystyle {\begin{array}{ccccccccc}0&\to &K_{n}&{\xrightarrow {F_{n))}&L_{n}&{\xrightarrow {G_{n))}&M_{n}&\to &0\\&&d'_{n}\downarrow \quad &&d_{n}\downarrow \quad &&d''_{n}\downarrow \quad &&\\0&\to &K_{n-1}&{\xrightarrow {F_{n-1))}&L_{n-1}&{\xrightarrow {G_{n-1))}&M_{n-1}&\to &0\end{array))}$

в якій рядки є точними послідовностями.

Звідси одержується комутативна діаграма

${\displaystyle {\begin{array}{ccccccccc}&&{\frac {K_{n)){B_{n}(K)))&{\xrightarrow {F_{n))}&{\frac {L_{n)){B_{n}(L)))&{\xrightarrow {G_{n))}&{\frac {M_{n)){B_{n}(M)))&\to &0\\&&{\bar {d'_{n))}\downarrow \quad &&{\bar {d_{n))}\downarrow \quad &&{\bar {d''_{n))}\downarrow \quad &&\\0&\to &Z_{n-1}(K)&{\xrightarrow {F_{n-1))}&Z_{n-1}(L)&{\xrightarrow {G_{n-1))}&Z_{n-1}(M)&&\end{array))}$

У цій діаграмі вертикальні відображення породжуються граничними відображеннями ланцюгових комплексів. Наприклад ${\displaystyle {\bar {d_{n))}:{\frac {L_{n)){B_{n}(L)))\to Z_{n-1}(L)}$визначається як:

${\displaystyle {\bar {d_{n))}(\alpha +B_{n}(L))=d_{n}(\alpha ).}$

Очевидно ${\displaystyle \ker {\bar {\partial _{n))}=H_{n}(L)}$ і ${\displaystyle \operatorname {coker} {\bar {\partial _{n))}=H_{n-1}(L),}$ тому з леми про змію відразу випливає існування гомоморфізмів ${\displaystyle \partial _{n}.}$

• Ланцюговий комплекс
• Точна послідовність
• 5-лема

• M. F. Atiyah, I. G. Macdonald: Introduction to Commutative Algebra. Oxford 1969, Addison–Wesley Publishing Company, Inc. ISBN 0-201-00361-9.
• P. Hilton; U. Stammbach: A course in homological algebra. 2. Auflage, Springer Verlag, Graduate Texts in Mathematics, 1997, ISBN 0-387-94823-6
• Serge Lang: Algebra. 3rd edition, Springer 2002, ISBN 978-0-387-95385-4, pp. 157–159 (online copy, с. 157, на «Google Books»)
• Northcott, D. G. A first course of homological algebra. Reprint of 1973 edition. Cambridge University Press, Cambridge-New York, 1980. ISBN 0-521-29976-4