Златен пресек (φ)

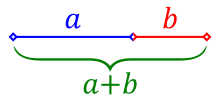Отсечки во златен пресек
Записи
Десетично	1,618033988749894...[1]
Алгебарски облик	${\displaystyle {\frac {1+{\sqrt {5))}{2))}$
Верижна дропка	${\displaystyle 1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\ddots ))))))))}$
Двоично	1,10011110001101110111...
Шеснаесетеречно	1,9E3779B97F4A7C15...

Во математиката две величини се во златниот однос ако соодносот помеѓу двете величини е еднаков на збирот на тие две вредности, наспроти повисоки вредности. Сликата од десно ја илустрира геометриски односи. Алгебарски, за количините a и b и a > b > 0,

${\displaystyle {\frac {a+b}{a))={\frac {a}{b))\ {\stackrel {\text{def)){=))\ \varphi ,}$

грчката буква фи (${\displaystyle \varphi }$ ili ${\displaystyle \phi }$) е константна. Неговата вредност е:

${\displaystyle \varphi ={\frac {1+{\sqrt {5))}{2))=1,6180339887\ldots .}$^[1]

Златниот однос се нарекува и  златен пресек (латински: sectio aurea).. Други имиња вклучуваат екстремен однос, среден пресек, златен сразмер, златен број. божествен пресек. Тоа е однос во кој има примена на предмети, слики итн. Предизвикува особено естетско доживување – допаѓање, па оттука е и името „Божествен пресек“.

Златниот однос се појавува во одредени модели во природата, вклучувајќи phyllotaxis (спирално сортирање листови) и други делови на растенија.

Математичарите уште во времето на Евклид ги изучувале својствата на златниот однос, вклучувајќи ја и појавата на мерење на правилен петаголник и на златниот правоаголник, што всушност може да се подели во квадрат и уште еден правоаголник на истиот однос.

Две величини a и b се во златниот однос φ ако

${\displaystyle {\frac {a+b}{a))={\frac {a}{b))=\varphi .}$

Еден начин да се најде вредноста на φ е со решавање на левата страна. Со упростување на прекршокот и со замена во b/a = 1/φ,

${\displaystyle {\frac {a+b}{a))=1+{\frac {b}{a))=1+{\frac {1}{\varphi )).}$

Затоа,

${\displaystyle 1+{\frac {1}{\varphi ))=\varphi .}$

Множење со φ дава

${\displaystyle \varphi +1=\varphi ^{2))$

што може да се изрази како

${\displaystyle {\varphi }^{2}-\varphi -1=0.}$

Со користење на формулата за решавање на  квадратни равенки, се добиваат две решенија:

${\displaystyle \varphi ={\frac {1+{\sqrt {5))}{2))=1,61803\,39887\dots }$

и

${\displaystyle \varphi ={\frac {1-{\sqrt {5))}{2))=-0,6180\,339887\dots }$

Бидејќи φ е однос меѓу двете позитивни вредности  φ е секогаш позитивна вредност:

${\displaystyle \varphi ={\frac {1+{\sqrt {5))}{2))=1,61803\,39887\dots }$ .

Златниот сооднос е ирационален број. Подолу се два кратки докази на ирационалната:

Да се потсетиме дека:

целината е подолг дел плус пократок дел;

целината е подолг дел, како што е подолг дел на пократок дел.

Ако некој број се нарекува n а подолгиот дел m, тогаш втората изјава станува:

n спроти m , исто како што и m спроти n − m,

или, во алгебрата:

${\displaystyle {\frac {n}{m))={\frac {m}{n-m)).\qquad (*)}$

Да се каже дека φ е рационално значи дека φ односите n/m каде n и m се integers. Ние може да се каже дека n/m имаат најниски вредности, и дека n и m се позитивни броеви. Но, ако дел n/m ниските вредности, тогаш идентитетот на белешки со (*) до врвот равенката m/(n − m), кој продолжува да имаат најниски вредности. Оваа контрадикција, која произлегува од тврдат дека φ е рационално.

Уште еден краток доказ — можеби и повеќе познати — каде што златната ирационалност на односот се користи како затвореност кај  рационалните броеви, собирање и множење. Ако ${\displaystyle }$ е рационално, и ${\displaystyle }$ е рационално, што е спроти фактите дека квадратниот корен од не квадратен природен број е ирационален.

Златниот сооднос е, исто така, алгебарски број, па дури и цел алгебарски број. Најмалиот полином гласи на следниот начин:

${\displaystyle x^{2}-x-1.}$

Поради членот со степен 2, овој полином всушност има два корени, и другата вреденост е роднина на златниот сооднос.

Други корени од најмалите полиноми x -² - x - 1

${\displaystyle -{\frac {1}{\varphi ))=1-\varphi ={\frac {1-{\sqrt {5))}{2))=-0.61803\,39887\dots .}$

Апсолутната вредност на оваа количина (≈ 0.618) одговара на должината на односите во обратна насока (должината на пократката страна во однос на подолгата, b/a), е понекогаш познат под името роднина на златниот пресек.^[2] Се означува со голема буква Фи (${\displaystyle \Phi }$):

${\displaystyle \Phi ={1 \over \varphi }=\varphi ^{-1}=0.61803\,39887\ldots .}$

• Златен правоаголник
• Сребрен пресек

п р у Ирационални броеви Хајтинов (Ω) Лиувилов Простоброen (ρ) Омега Каенов Логаритам од 2 Гаусов (G) Дванаесетти корен од 2 Апериев (ζ(3)) Пластичен (ρ) Квадратен корен од 2 Суперзлатен пресек (ψ) Ердеш-Борвејнов (E) Златен пресек (φ) Квадратен корен од 3 Квадратен корен од 5 Сребрен пресек (δS) Квадратен корен од 6 Квадратен корен од 7 Ојелров (e) Пи (π) Шизофрен Трансцендентен Тригонометриски