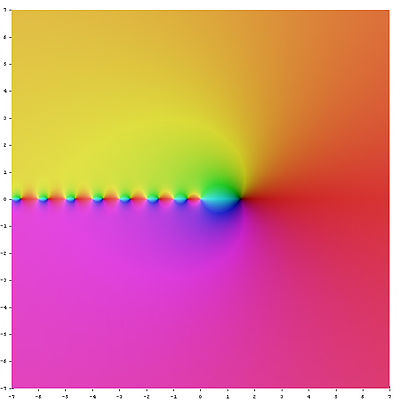
Digamma-függvény a komplex síkon: a színek kódolják az s értékét, erősebb színek a zéró közeli értékeket mutatják A ψ (x ) jelű digamma-függvény a gamma-függvény logaritmikus deriváltja .
ψ
(
x
)
=
d
d
x
ln
Γ
(
x
)
=
Γ
′
(
x
)
Γ
(
x
)
.
{\displaystyle \psi (x)={\frac {d}{dx))\ln {\Gamma (x)}={\frac {\Gamma '(x)}{\Gamma (x))).}
Ez az első poligamma-függvény .
A digamma-függvény (jelölései: ψ0 (x ), ψ0 (x ), vagy
ϝ
{\displaystyle \digamma }
digamma (Ϝ ϝ) a preklasszikus görög ábécé hatodik betűje után) következőképpen kapcsolódik a harmonikus számokhoz :
ψ
(
n
)
=
H
n
−
1
−
γ
{\displaystyle \psi (n)=H_{n-1}-\gamma \!}
ahol H n n -edik harmonikus szám, és γ az Euler-Mascheroni konstans.
Félegész értékekre:
ψ
(
n
+
1
2
)
=
−
γ
−
2
ln
2
+
∑
k
=
1
n
2
2
k
−
1
{\displaystyle \psi \left(n+{\frac {1}{2))\right)=-\gamma -2\ln 2+\sum _{k=1}^{n}{\frac {2}{2k-1))}
ψ
(
x
)
=
∫
0
∞
(
e
−
t
t
−
e
−
x
t
1
−
e
−
t
)
d
t
{\displaystyle \psi (x)=\int _{0}^{\infty }\left({\frac {e^{-t)){t))-{\frac {e^{-xt)){1-e^{-t))}\right)\,dt}
ez a kifejezés akkor érvényes, ha
x
{\displaystyle x}
Kifejezhetjük:
ψ
(
s
+
1
)
=
−
γ
+
∫
0
1
1
−
x
s
1
−
x
d
x
{\displaystyle \psi (s+1)=-\gamma +\int _{0}^{1}{\frac {1-x^{s)){1-x))dx}
mely megfelel az Euler-integrálnak harmonikus számokra.
A digamma kiszámolható a komplex síkon a negatív egészeken kívül a következő képlettel:
ψ
(
z
+
1
)
=
−
γ
+
∑
n
=
1
∞
z
n
(
n
+
z
)
z
≠
−
1
,
−
2
,
−
3
,
…
{\displaystyle \psi (z+1)=-\gamma +\sum _{n=1}^{\infty }{\frac {z}{n(n+z)))\qquad z\neq -1,-2,-3,\ldots }
vagy
ψ
(
z
)
=
−
γ
+
∑
n
=
0
∞
z
−
1
(
n
+
1
)
(
n
+
z
)
=
−
γ
+
∑
n
=
0
∞
(
1
n
+
1
−
1
n
+
z
)
z
≠
0
,
−
1
,
−
2
,
−
3
,
…
{\displaystyle \psi (z)=-\gamma +\sum _{n=0}^{\infty }{\frac {z-1}{(n+1)(n+z)))=-\gamma +\sum _{n=0}^{\infty }\left({\frac {1}{n+1))-{\frac {1}{n+z))\right)\qquad z\neq 0,-1,-2,-3,\ldots }
Ez felhasználható racionális függvények végtelen szummájának számítására, például:
∑
n
=
0
∞
u
n
=
∑
n
=
0
∞
p
(
n
)
q
(
n
)
{\displaystyle \sum _{n=0}^{\infty }u_{n}=\sum _{n=0}^{\infty }{\frac {p(n)}{q(n)))}
ahol p (n ) és q (n ) n polinomjai.
Magasabb rendű poligamma-függvény sor kiterjesztésével, egy általánosított képlet kapható:
∑
n
=
0
∞
u
n
=
∑
n
=
0
∞
∑
k
=
1
m
a
k
(
n
+
b
k
)
r
k
=
∑
k
=
1
m
(
−
1
)
r
k
(
r
k
−
1
)
!
a
k
ψ
(
r
k
−
1
)
(
b
k
)
,
{\displaystyle \sum _{n=0}^{\infty }u_{n}=\sum _{n=0}^{\infty }\sum _{k=1}^{m}{\frac {a_{k)){(n+b_{k})^{r_{k))))=\sum _{k=1}^{m}{\frac {(-1)^{r_{k))}{(r_{k}-1)!))a_{k}\psi ^{(r_{k}-1)}(b_{k}),}
feltéve, ha a sorozat bal oldala konvergens.
A digammának van egy racionális zéta sorozata, mely a Taylor-sorból ered z =1-nél. Ez:
ψ
(
z
+
1
)
=
−
γ
−
∑
k
=
1
∞
ζ
(
k
+
1
)
(
−
z
)
k
{\displaystyle \psi (z+1)=-\gamma -\sum _{k=1}^{\infty }\zeta (k+1)\;(-z)^{k))
mely konvergál |z |<1 felé. Itt a
ζ
(
n
)
{\displaystyle \zeta (n)}
Riemann-féle zéta-függvény .
A digamma Newton-sora az Euler integrál képletből adódik:
ψ
(
s
+
1
)
=
−
γ
−
∑
k
=
1
∞
(
−
1
)
k
k
(
s
k
)
{\displaystyle \psi (s+1)=-\gamma -\sum _{k=1}^{\infty }{\frac {(-1)^{k)){k)){s \choose k))
ahol
(
s
k
)
{\displaystyle \textstyle {s \choose k))
binomiális együttható .
A digamma-függvény reflexiós képlete hasonló a gamma-függvényével.
ψ
(
1
−
x
)
−
ψ
(
x
)
=
π
cot
(
π
x
)
{\displaystyle \psi (1-x)-\psi (x)=\pi \,\!\cot {\left(\pi x\right)))
A digamma Gauss-összege :
−
1
π
k
∑
n
=
1
k
sin
(
2
π
n
m
k
)
ψ
(
n
k
)
=
ζ
(
0
,
m
k
)
=
−
B
1
(
m
k
)
=
1
2
−
m
k
{\displaystyle {\frac {-1}{\pi k))\sum _{n=1}^{k}\sin \left({\frac {2\pi nm}{k))\right)\psi \left({\frac {n}{k))\right)=\zeta \left(0,{\frac {m}{k))\right)=-B_{1}\left({\frac {m}{k))\right)={\frac {1}{2))-{\frac {m}{k))}
0
<
m
<
k
{\displaystyle 0<m<k}
s ,q ) a Hurwitz zéta függvény, és a
B
n
(
x
)
{\displaystyle B_{n}(x)}
Gauss digamma elmélete,[ 1] [ 2] m és k ( m < k ), pozitív egészekre, a digamma függvény elemi függvényekkel is kifejezhető:
ψ
(
m
k
)
=
−
γ
−
ln
(
2
k
)
−
π
2
cot
(
m
π
k
)
+
2
∑
n
=
1
⌊
(
k
−
1
)
/
2
⌋
cos
(
2
π
n
m
k
)
ln
(
sin
(
n
π
k
)
)
{\displaystyle \psi \left({\frac {m}{k))\right)=-\gamma -\ln(2k)-{\frac {\pi }{2))\cot \left({\frac {m\pi }{k))\right)+2\sum _{n=1}^{\lfloor (k-1)/2\rfloor }\cos \left({\frac {2\pi nm}{k))\right)\ln \left(\sin \left({\frac {n\pi }{k))\right)\right)}
J.-M. Bernardo AS 103 algoritmusa szerint[ 3] x valós számokra közelíthető:
ψ
(
x
)
=
ln
(
x
)
−
1
2
x
−
1
12
x
2
+
1
120
x
4
−
1
252
x
6
+
O
(
1
x
8
)
{\displaystyle \psi (x)=\ln(x)-{\frac {1}{2x))-{\frac {1}{12x^{2))}+{\frac {1}{120x^{4))}-{\frac {1}{252x^{6))}+O\left({\frac {1}{x^{8))}\right)}
Hasonló közelítés magasabb tagokra:
ψ
(
x
)
=
ln
(
x
)
−
1
2
x
−
1
12
x
2
+
1
120
x
4
−
1
252
x
6
+
1
240
x
8
−
5
660
x
10
+
691
32760
x
12
−
7
84
x
14
+
3617
8160
x
16
−
43867
14364
x
18
+
O
(
1
x
20
)
{\displaystyle {\begin{aligned}\psi (x)&=\ln(x)-{\frac {1}{2x))-{\frac {1}{12x^{2))}+{\frac {1}{120x^{4))}-{\frac {1}{252x^{6))}+{\frac {1}{240x^{8))}-{\frac {5}{660x^{10))}\\&\quad +{\frac {691}{32760x^{12))}-{\frac {7}{84x^{14))}+{\frac {3617}{8160x^{16))}-{\frac {43867}{14364x^{18))}+O\left({\frac {1}{x^{20))}\right)\end{aligned))}
Gauss digamma elmélete eredményeképpen a digamma-függvény zárt formájú értékei racionális számokra :
ψ
(
1
)
=
−
γ
{\displaystyle \psi (1)=-\gamma \,\!}
ψ
(
1
2
)
=
−
2
ln
2
−
γ
{\displaystyle \psi \left({\frac {1}{2))\right)=-2\ln {2}-\gamma }
ψ
(
1
3
)
=
−
π
2
3
−
3
2
ln
3
−
γ
{\displaystyle \psi \left({\frac {1}{3))\right)=-{\frac {\pi }{2{\sqrt {3))))-{\frac {3}{2))\ln {3}-\gamma }
ψ
(
1
4
)
=
−
π
2
−
3
ln
2
−
γ
{\displaystyle \psi \left({\frac {1}{4))\right)=-{\frac {\pi }{2))-3\ln {2}-\gamma }
ψ
(
1
6
)
=
−
π
2
3
−
2
ln
2
−
3
2
ln
(
3
)
−
γ
{\displaystyle \psi \left({\frac {1}{6))\right)=-{\frac {\pi }{2)){\sqrt {3))-2\ln {2}-{\frac {3}{2))\ln(3)-\gamma }
ψ
(
1
8
)
=
−
π
2
−
4
ln
2
−
1
2
{
π
+
ln
(
2
+
2
)
−
ln
(
2
−
2
)
}
−
γ
{\displaystyle \psi \left({\frac {1}{8))\right)=-{\frac {\pi }{2))-4\ln {2}-{\frac {1}{\sqrt {2))}\left\{\pi +\ln(2+{\sqrt {2)))-\ln(2-{\sqrt {2)))\right\}-\gamma }
Abramowitz, M.; Stegun, I. A., eds: "6.3 psi (Digamma) Function.". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. (hely nélkül): New York: Dover. 1972. 258–259. o.
Bernardo, José M: "Algorithm AS 103 psi(digamma function) computation". (hely nélkül): Applied Statistics 25. 1976. 315–317. o.