במתמטיקה, אלגברת האוקטוניונים היא אלגברת החילוק האלטרנטיבית היחידה מממד 8 מעל שדה המספרים הממשיים. אלגברה זו, שאינה אסוציאטיבית, היא אלגברת האוקטוניונים הידועה ביותר. מקובל לסמן את המבנה באות ${\displaystyle \mathbb {O} }$.

אלגברת האוקטוניונים קשורה למספר מבנים מתמטיים יוצאי דופן, ובהם חבורות לי מטיפוס ${\displaystyle G_{2))$. בנוסף, לאוקטוניונים יש שימושים בתחומים כגון תורת המיתרים ותורת היחסות הפרטית.

את האוקטוניונים גילה בשנת 1843 ג'ון ט. גרייבס, חבר של ויליאם המילטון, לאחר שהלה בנה את אלגברת הקווטרניונים של המילטון; גרייבס קרא להם אוקטבות, ושם זה עדיין נמצא בשימוש.

ארתור קיילי גילה את האוקטוניונים באופן בלתי תלוי, ופרסם אותם לראשונה בשנת 1845. האוקטוניונים מוכרים לעיתים כמספרי קיילי.

האוקטוניונים הם, כאמור, אלגברה מממד 8 מעל שדה המספרים הממשיים. כל אוקטוניון הוא צירוף ליניארי של אוקטוניוני היחידה ${\displaystyle \left\{1,i,j,ij,l,il,jl,(ij)l\right\))$, כלומר, כל אוקטוניון אפשר לכתוב בצורה ${\displaystyle x=x_{0}+x_{1}i+x_{2}j+x_{3}ij+x_{4}l+x_{5}il+x_{6}jl+x_{7}(ij)l}$, כאשר ${\displaystyle x_{0},\dots ,x_{7))$ הם מקדמים ממשיים.

חיבור אוקטוניונים מתבצע על ידי חיבור המקדמים. הכפל נקבע לפי לוח הכפל של אוקטוניוני היחידה (הגורמים משמאל הוא זה המוצג בראש השורה):

1	${\displaystyle i}$	${\displaystyle j}$	${\displaystyle ij}$	${\displaystyle l}$	${\displaystyle il}$	${\displaystyle jl}$	${\displaystyle (ij)l}$
${\displaystyle i}$	−1	${\displaystyle ij}$	-${\displaystyle j}$	${\displaystyle il}$	-${\displaystyle l}$	-${\displaystyle (ij)l}$	${\displaystyle jl}$
${\displaystyle j}$	${\displaystyle -ij}$	−1	${\displaystyle i}$	${\displaystyle jl}$	${\displaystyle (ij)l}$	-${\displaystyle l}$	-${\displaystyle il}$
${\displaystyle ij}$	${\displaystyle j}$	-${\displaystyle i}$	−1	${\displaystyle (ij)l}$	${\displaystyle -jl}$	${\displaystyle il}$	-${\displaystyle l}$
${\displaystyle l}$	-${\displaystyle il}$	${\displaystyle -jl}$	-${\displaystyle (ij)l}$	−1	${\displaystyle i}$	${\displaystyle j}$	${\displaystyle ij}$
${\displaystyle il}$	${\displaystyle l}$	-${\displaystyle (ij)l}$	${\displaystyle jl}$	-${\displaystyle i}$	−1	-${\displaystyle ij}$	${\displaystyle j}$
${\displaystyle jl}$	${\displaystyle (ij)l}$	${\displaystyle l}$	-${\displaystyle il}$	-${\displaystyle j}$	${\displaystyle ij}$	−1	-${\displaystyle i}$
${\displaystyle (ij)l}$	${\displaystyle -jl}$	${\displaystyle il}$	${\displaystyle l}$	${\displaystyle -ij}$	-${\displaystyle j}$	${\displaystyle i}$	−1

כך אפשר לראות שאלגברת האוקטוניונים אינה קומוטטיבית (${\displaystyle ij=-ji\neq ji}$) ואינה אסוציאטיבית (${\displaystyle \left(ij\right)l=-i\left(jl\right)\neq i\left(jl\right)}$). בחירת הבסיס אינה קנונית - בסיסים סטנדרטיים אחרים נבדלים מן הבסיס שהוצג לעיל בסדר האיברים ובסימן המכפלות.

אפשר לבנות את האוקטוניונים באופן שיטתי, מאלגברת הקווטרניונים של המילטון, באמצעות בניית קיילי-דיקסון. בבניה זו, כפי שמספרים מרוכבים הם זוגות של מספרים ממשיים וקווטרניונים הם זוגות של מספרים מרוכבים, כל אוקטוניון הוא זוגות של קווטרניונים. החיבור, כתמיד, הוא לפי רכיבים. כפל של שני זוגות קווטרניונים ${\displaystyle \left(a,b\right)}$ ו-${\displaystyle \left(c,d\right)}$ מתבצע כך:
${\displaystyle \left(a,b\right)\left(c,d\right)=\left(ac-{\bar {d))b,da+b{\bar {c))\right)}$
כאשר ${\displaystyle {\bar {z))}$ מסמל את הצמוד של הקווטרניון ${\displaystyle z}$. הגדרה זו שקולה לקודמת, כאשר אוקטוניוני היחידה הם:
${\displaystyle \left(1,0\right),\left(i,0\right),\left(j,0\right),\left(ij,0\right),\left(0,1\right),\left(0,i\right),\left(0,j\right),\left(0,ij\right)}$.

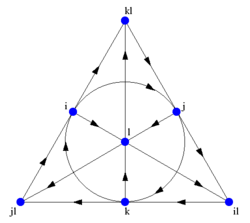
עזר זיכרון נוח שמאפשר לזכור את המכפלות של אוקטוניוני היחידה נתון בדיאגרמה שלהלן. דיאגרמה זו בעלת 7 נקודות ו-7 קווים (המעגל בין i, j ו-ij נחשב כקו) נקראת מישור פאנו. לקווים יש כיוון בדיאגרמה זאת. שבע הנקודות מתאימות לשבעת גורמי הבסיס של ${\displaystyle \Im \left(\mathbb {O} \right)}$. כל זוג נקודות נמצא על קו יחיד, ועל כל קו יש בדיוק שלוש נקודות.

ניקח ${\displaystyle a,\ b,\ c}$ בתור שלישיית נקודות שנמצאות על קו ומסודרות לפי כיווני החצים. הכפל מתבצע על ידי
${\displaystyle ab=c}$ וגם ${\displaystyle ba=-c}$
ביחד עם תמורה מחזורית. כלל זה ביחד עם:

• 1 הוא היחידה הכפלית,
• ${\displaystyle e^{2}=-1}$ לכל נקודה בדיאגרמה

מגדירים לגמרי את מבנה הכפל של האוקטוניונים. כל קו יוצר תת-אלגברה של ${\displaystyle \mathbb {O} }$ שהיא איזומורפית לאלגברת הקווטרניונים. למעשה, כל תת-אלגברה של ${\displaystyle \mathbb {O} }$ היא אחת מאלגברות ההרכב ${\displaystyle \mathbb {R} }$, ${\displaystyle \mathbb {C} }$, או ${\displaystyle \mathbb {H} }$.

הצמוד של אוקטוניון
${\displaystyle x=x_{0}+x_{1}i+x_{2}j+x_{3}ij+x{4}l+x{5}il+x{6}jl+x{7}(ij)l}$
נתון על ידי:
${\displaystyle {\bar {x))=x_{0}-x_{1}i-x_{2}j-x_{3}ij-x_{4}l-x_{5}il-x_{6}jl-x_{7}(ij)l}$
ההצמדה היא אינוולוציה: ${\displaystyle {\overline {\left(xy\right)))={\bar {y)){\bar {x))}$, ו- ${\displaystyle {\overline {\overline {x))}=x}$.

החלק הממשי של ${\displaystyle x}$ מחושב על ידי ${\displaystyle {\frac {x+{\bar {x))}{2))=x_{0))$, והחלק המדומה (השבעה-ממדי) - על ידי ${\displaystyle {\frac {x-{\bar {x))}{2))}$.

הנורמה באלגברת האוקטוניונים מוגדרת לפי ${\displaystyle \left\|x\right\|={\bar {x))x}$, וזהו תמיד מספר ממשי לא-שלילי: ${\displaystyle \left\|x\right\|={\bar {x))x=x_{0}^{2}+x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}+x_{5}^{2}+x_{6}^{2}+x_{7}^{2))$. (לפעמים מעוניינים בשורש של הנורמה האלגברית, שהוא האורך של הווקטור במרחב האוקלידי השמונה-ממדי).

למרות שהאלגברה אינה אסוציאטיבית, הנורמה היא פונקציה כפלית, וכך נעשית אלגברת האוקטוניונים אלגברת הרכב. עובדה זו אחראית במידה רבה לנוסחת הכפל הפולינומית עבור סכומים של שמונה ריבועים (ראו משפט הורוויץ על תבניות ריבועיות; נוסחת כפל רציונלית נובעת מכך שסכום הריבועים הוא תבנית פיסטר). הנורמה גם מאפשרת לחשב את ההפכי לכל איבר: ההופכי של ${\displaystyle x\neq 0}$ נתון על ידי: ${\displaystyle x^{-1}={\frac {\bar {x)){\left\|x\right\|))}$.

• אלגברות קיילי-דיקסון

מדיה וקבצים בנושא אלגברת האוקטוניונים של קיילי בוויקישיתוף

• אלגברת האוקטוניונים של קיילי, באתר MathWorld (באנגלית)

מערכות מספרים
מספרים	המספרים הטבעיים ${\displaystyle \mathbb {N} }$ (מערכת פאנו) • חוג המספרים השלמים ${\displaystyle \mathbb {Z} }$ (מספרים חיוביים ושליליים, מספר שלם) • שדה המספרים הרציונליים ${\displaystyle \mathbb {Q} }$ (מספר רציונלי, מספר אי-רציונלי) • שדה המספרים הממשיים ${\displaystyle \mathbb {R} }$ (הישר הממשי, מספר ממשי) • שדה המספרים המרוכבים ${\displaystyle \mathbb {C} }$ (המישור המרוכב, מספר מרוכב, מספר מדומה)
הרחבות של חוג המספרים השלמים	חוג השלמים של גאוס ${\displaystyle \ \mathbb {Z} [i]}$ • חוג השלמים האלגבריים ${\displaystyle \ {\overline {\mathbb {Z} ))}$ • חוג השלמים של אייזנשטיין ${\displaystyle \ \mathbb {Z} [\omega ]}$
הרחבות של שדה המספרים הרציונליים	שדה מספרים • שדה המספרים הניתנים לבנייה • שדה המספרים האלגבריים ${\displaystyle \ {\overline {\mathbb {Q} ))}$ (מספר אלגברי, מספר טרנסצנדנטי) • שדה המספרים ה-p-אדיים ${\displaystyle \mathbb {Q} _{p))$ (מספר p-אדי) • שדה ציקלוטומי
מעבר למרוכבים	אלגברת קווטרניונים (אלגברת הקווטרניונים של המילטון ${\displaystyle \ {\mathbb {H} ))$) • אלגברת אוקטוניונים (אלגברת האוקטוניונים של קיילי ${\displaystyle \ {\mathbb {O} ))$) • אלגברות קיילי-דיקסון