IEEE 754
El estándar del IEEE para aritmética en punto flotante (IEEE 754) es la norma o estándar técnico para computación en punto flotante, establecida en 1985 por el Instituto de Ingenieros Eléctricos y Electrónicos (IEEE). La norma abordó muchos problemas encontrados en las diversas implementaciones de punto flotante que las hacían difíciles de usar de forma fiable y portátil. Muchas unidades de coma flotante de hardware utilizan ahora el estándar IEEE 754.
El estándar define:
- Formatos aritméticos: conjuntos de datos de punto flotante binarios y decimales, que consisten en números finitos, incluidos los ceros con signo y los números desnormalizados o subnormales, infinitos y valores especiales "no numéricos" (NaN).
- Formatos de intercambio: codificaciones (cadenas de bits) que se pueden utilizar para intercambiar datos de punto flotante de forma eficiente y compacta.
- Reglas de redondeo: propiedades que deben satisfacerse al redondear los números durante las operaciones aritméticas y las conversiones.
- Operaciones: operaciones aritméticas y otras (como funciones trigonométricas) en formatos aritméticos.
- Manejo de excepciones: indicaciones de condiciones excepcionales, tales como división por cero, desbordamiento, etc.
La norma también es conocida como IEC 60559:1989, Binary floating-point arithmetic for microprocessor systems (originalmente el número de referencia era IEC 559:1989).[1]
La versión actual, IEEE 754-2008 publicada en agosto de 2008, incluye casi todo el estándar IEEE 754-1985 original y el estándar IEEE para aritmética de punto flotante independiente de la base (IEEE 854-1987).
Desarrollo del estándar
[editar]La versión actual del estándar, denominada IEEE 754-2008, publicada en agosto de 2008, se deriva de la versión anterior (IEEE 754-1985) a la cual seguida por un proceso de revisión de siete años, presidido por Dan Zuras y editado por el profesor de ciencias de la computación Mike Cowlishaw.
El estándar internacional ISO/IEC/IEEE 60559:2011, con contenido idéntico al IEEE 754-2008 ha sido aprobado para su adopción a través del comité técnico conjunto ISO/IEC JTC 1/SC 25 en virtud del acuerdo ISO/IEEE PSDO[2] y publicado.[3]
Los formatos binarios en el estándar original se incluyen en el nuevo estándar junto con tres nuevos formatos básicos (uno binario y dos decimales). Para cumplir con el estándar actual, debe ser implementado al menos uno de los formatos básicos tanto como formato aritmético, como de intercambio. En septiembre de 2015, la norma empezó a ser revisada para incorporar aclaraciones y erratas.[4][5]
Formatos
[editar]Un formato IEEE 754 es un conjunto de representaciones de valores numéricos y símbolos. Un formato también puede incluir cómo se codifica el conjunto.
Un formato comprende:
- Números finitos, que pueden ser de base 2 (binario) o de base 10 (decimal). Cada número finito se describe por tres enteros: s (un bit de signo), c (un significando, mantisa o coeficiente) y q (exponente). El valor numérico de un número finito es:
Donde b es la base (2 o 10). Por ejemplo, si la base es 10, el signo es 1 (lo que indica signo negativo), el significando es 12345, y el exponente es -3, entonces el valor del número es: (−1)1 × 12345 × 10−3 = −1 × 12345 × .001 = −12.345.
- Dos infinitos: y .
- Dos tipos de valores no numéricos (NaN): un NaN silencioso (qNaN) y un NaN de señalización (sNaN). Un NaN puede llevar una carga útil que está destinada a la información de diagnóstico que indica la fuente de la NaN. El signo de un NaN no tiene sentido, pero puede ser predecible en algunas circunstancias.
Los posibles valores finitos que se pueden representar en un formato están determinados por la base , el número de dígitos en el significando (precisión p) y el parámetro exponente máximo :
- c debe ser un número entero en el intervalo cerrado . Por ejemplo, si b = 10 y p = 7 entonces c está en el intervalo cerrado [0, 9999999]).
- q debe ser un entero tal que . Si p = 7 y emax = 96 entonces q está en el intervalo cerrado [-101, 90].
Por lo tanto (para los parámetros del ejemplo) el número positivo no nulo más pequeño que se puede representar es 1 × 10-101 y el más grande es 9999999 × 1090 (9,999999 × 1096), y el rango completo de números está en el intervalo [-9,999999 × 1096 a 9,999999 × 1096]. Los números -b1-emax y b1-emax (en este ejemplo, -1 × 10-95 y 1 × 10-95) son los números normales más pequeños (en magnitud); los números no nulos entre estos números más pequeños se llaman números subnormales.
Los valores ceros son valores finitos con significando 0. Estos son ceros con signo, el bit de signo específica si un cero es +0 (cero positivo) o -0 (cero negativo).
Representación y codificación en memoria
[editar]Algunos números pueden tener varias representaciones en el modelo que acaba de ser descrito. Por ejemplo, si b = 10 y p = 7, entonces el número -12,345 puede representarse como -12345 × 10-3, -123450 × 10-4 y -1234500 × 10-5. Sin embargo, para la mayoría de las operaciones, como las operaciones aritméticas, el resultado (valor) no depende de la representación de las entradas.
Para los formatos decimales, cualquier representación es válida, y el conjunto de estas representaciones se llama cohorte. Cuando un resultado puede tener varias representaciones, el estándar específica qué miembro de la cohorte es elegido.
Para los formatos binarios, la representación se hace única eligiendo el exponente representable más pequeño. Para los números con un exponente en el rango normal (no todos unos o todos ceros), el bit inicial del significando siempre será 1. En consecuencia, el bit 1 principal puede ser implícito en lugar de estar explícitamente presente en la codificación de la memoria. Esta regla se denomina convención de bit principal, o también convención de bits implícita o convención de bits ocultos. La regla permite que el formato de memoria tenga un poco más de precisión. La convención de bit principal no se utiliza para los números subnormales ya que tienen un exponente fuera del rango del exponente normal.
Formatos básicos y de intercambio
[editar]El estándar IEEE 754 define cinco formatos básicos que se denominan por su base numérica y el número de bits utilizados en su codificación de intercambio. Existen tres formatos básicos binarios de punto flotante (codificados con 32, 64 o 128 bits) y dos formatos básicos de punto flotante decimal (codificados con 64 o 128 bits). Los formatos binary32 y binary64 son los formatos simple y doble del estándar original IEEE 754-1985. Una implementación conforme debe implementar completamente al menos uno de los formatos básicos.
El estándar también define los formatos de intercambio, que generalizan estos formatos básicos.[6] Para los números binarios, se requiere la convención de bit de entrada. La siguiente tabla resume los formatos de intercambio más pequeños (incluidos los más básicos).
| Nombre | Nombre común | Base | Dígitos | Dígitos
decimales |
Bits del Exponente | Emax
Decimal |
Sesgo del
Exponente[7] |
Emin | Emax | Notas |
|---|---|---|---|---|---|---|---|---|---|---|
| binary16 | Media precisión | 2 | 11 | 3,31 | 5 | 4,51 | 24−1 = 15 | −14 | +15 | No básico |
| binary32 | Simple precisión | 2 | 24 | 7,22 | 8 | 38,23 | 27−1 = 127 | −126 | +127 | |
| binary64 | Doble precisión | 2 | 53 | 15,95 | 11 | 307,95 | 210−1 = 1023 | −1022 | +1023 | |
| binary128 | Cuádruple precisión | 2 | 113 | 34,02 | 15 | 4931,77 | 214−1 = 16383 | −16382 | +16383 | |
| binary256 | Óctuple precisión | 2 | 237 | 71,34 | 19 | 78913,20 | 218−1 = 262143 | −262142 | +262143 | No básico |
| decimal32 | 10 | 7 | 7 | 7,58 | 96 | 101 | −95 | +96 | No básico | |
| decimal64 | 10 | 16 | 16 | 9,58 | 384 | 398 | −383 | +384 | ||
| decimal128 | 10 | 34 | 34 | 13,58 | 6144 | 6176 | −6143 | +6144 |
Obsérvese que, en la tabla anterior, los exponentes mínimos listados son para números normales. La representación de números subnormales especiales permite representar números aún más pequeños (con cierta pérdida de precisión). Por ejemplo, el menor número de doble precisión mayor que cero que se puede representar en esa forma es 2-1074 (porque 1074 = 1022 + 53 - 1). La cantidad de dígitos decimales es la cantidad de dígitos del número por el logaritmo decimal de la base, lo que da una precisión aproximada en decimal. La columna E max Decimal es Emax por el logaritmo decimal de la base, esto da el máximo exponente en decimal.
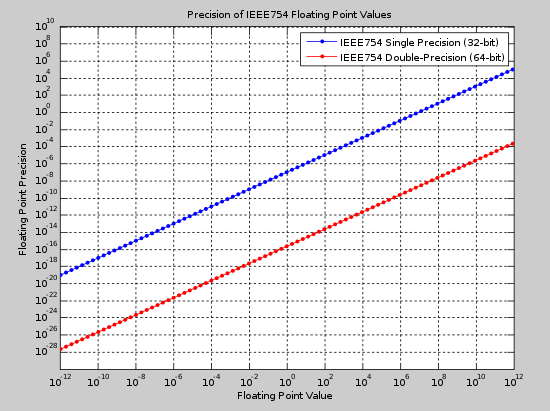
Como se indicó anteriormente, los formatos binary32 y binary64 son idénticos a los formatos simple y doble, respectivamente, del estándar origina IEEE 754-1985 y son dos de los formatos más comunes usados hoy en día. La figura siguiente muestra la precisión absoluta para los formatos binario32 y binario64 en el rango de 10-12 a 10+12. Tal figura puede usarse para seleccionar un formato apropiado, dado el valor esperado de un número y la precisión requerida.
Formatos de precisión extendidos y extensibles
[editar]El estándar de coma flotante IEEE específica formatos de precisión extendidos y extensibles, que se recomiendan para permitir una mayor precisión que la proporcionada por los formatos básicos.[6] Un formato de precisión extendido amplía un formato básico utilizando más precisión y más rango de exponentes. Un formato de precisión extensible, en cambio, permite al usuario especificar la precisión y el rango de exponentes. Una implementación puede usar cualquier representación interna que elija para tales formatos. Todo lo que necesita ser definido son sus parámetros (base, precisión y máximo exponente). Estos parámetros describen de manera única el conjunto de números finitos (combinaciones de signo, significante y exponente para la base dada) que puede representar.
La norma no requiere una implementación para soportar los formatos de precisión extendidos o extensibles, aunque recomienda que los lenguajes de programación proporcionen un método de especificación de la precisión y del máximo exponente para cada base e igualmente que los lenguajes y las implementaciones soporten un formato extendido que tenga una mayor precisión que el formato básico más grande soportado para cada base.[6]
Para un formato extendido con una precisión entre dos formatos básicos, el rango de exponentes debe ser tan grande como el del siguiente formato básico más amplio. Por ejemplo, un número binario de 64 bits de precisión extendida debe tener un exponente máximo de al menos 16383. El formato extendido x87 de 80 bits cumple este requisito.
Formatos de intercambio
[editar]Los formatos de intercambio están destinados al intercambio de datos de punto flotante utilizando una cadena de bits de longitud fija para un formato dado. Para el intercambio de números de punto flotante binaria, se definen formatos de intercambio de longitudes de 16 bits, 32 bits, 64 bits y cualquier múltiplo de 32 bits mayor o igual a 128. El formato de 16 bits está destinado al intercambio o almacenamiento de pequeños números (por ejemplo, para gráficos).
El esquema de codificación para estos formatos de intercambio binario es el mismo que el de la norma original IEEE 754-1985: un bit de signo seguido de w bits para el exponente compensado por un sesgo y p-1 bits que describen el significando. La anchura del campo de exponentes para un formato de k bits se calcula como sigue:
en la cual la función redondea el resultado al entero inferior próximo.
Los formatos existentes de 64 y 128 bits siguen esta regla, pero los formatos de 16 y 32 bits tienen más bits de exponentes (5 y 8) de lo que proporcionaría esta fórmula (3 y 7, respectivamente). Como ocurre con el estándar original IEEE 754-1985, hay cierta flexibilidad en la codificación de la señalización para las cadenas no numéricas o NaN.
Para el intercambio de números decimales de punto flotante, se definen formatos de cualquier múltiplo de 32 bits. El esquema de codificación para los formatos de intercambio decimal codifica de forma similar el signo, exponente y significando, pero se definen dos representaciones de nivel de bits diferentes. El intercambio es complicado por el hecho de que se requiere algún indicador externo de la representación en uso. Las dos opciones permiten que el significando sea codificado como una secuencia comprimida de dígitos decimales, usando decimales densamente empacados, o alternativamente como un entero binario. El primero es más conveniente para la implementación directa de hardware del estándar, mientras que el segundo es más adecuado para la emulación de software en un computador. En ambos casos, el conjunto de números (combinaciones de signo, significando y exponente) que pueden ser codificados es idéntico, y los valores especiales (± cero, ± infinito, NaNs silencioso y NaNs de señalización) tienen representaciones binarias idénticas.
Referencias
[editar]- ↑ «IEEE Std 1003.1, 2004 Edition» (en inglés). The Open Group. Consultado el 27 de febrero de 2017.
- ↑ «FW: ISO/IEC/IEEE 60559 (IEEE Std 754-2008)». grouper.ieee.org (en inglés). IEEE. 1 de abril de 2011. Archivado desde el original el 19 de marzo de 2012. Consultado el 18 de marzo de 2017.
- ↑ «ISO/IEC/IEEE 60559:2011 - Information technology -- Microprocessor Systems -- Floating-Point arithmetic». www.iso.org (en inglés). ISO. Consultado el 18 de marzo de 2017.
- ↑ «IEEE 754-2008 errata». speleotrove.com (en inglés). Archivado desde el original el 8 de octubre de 2019. Consultado el 18 de marzo de 2017.
- ↑ «Revising ANSI/IEEE Std 754-2008 http://754r.ucbtest.org». 754r.ucbtest.org (en inglés). Consultado el 18 de marzo de 2017.
- ↑ a b c «IEEE Std 754-2008: IEEE Standard for Floating-Point Arithmetic» (en inglés). IEEE Inc. Archivado desde el original el 6 de noviembre de 2016. Consultado el 27 de febrero de 2017.
- ↑ Mike Cowlishaw (20 de marzo de 2009). «Decimal Arithmetic Encodings» (en inglés). IBM UK Laboratories. Consultado el 18 de marzo de 2017.
Véase también
[editar]- Notación científica
- Coma flotante
- Tipo de dato real
- Intel 8087. El coprocesador numérico de donde surgió iniciativa para el estándar IEEE 754
Enlaces externos
[editar]- Referencias IEEE 754
- Let's Get To The (Floating) Point por Chris Hecker
- What Every Computer Scientist Should Know About Floating-Point Arithmetic by David Goldberg - una buena introducción y explicación.
- Curso de Representación de los Datos de Carlos Pes
- Comparing floating point numbers Bruce Dawson
- Calculadora de números binarios en coma flotante
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.






![{\displaystyle [0,b^{p}-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f9885dc8342d2bcb329a8855579e4236c02e5fe)



