En matemàtiques, específicament en topologia, l'interior d'un subconjunt S de punts d'un espai topològic X està format per tots els punts de S que no pertanyen a la frontera de S. Els punts de l'interior de S es denominen punts interiors de S.

L'interior de S és el complementari de la clausura del complementari de S. En aquest sentit, l'interior i la clausura són nocions duals.

L'exterior d'un conjunt és l'interior del complementari, o equivalentment el complementari de la clausura. Està format pels punts que no pertanyen ni al conjunt ni a la frontera. L'interior, la frontera i l'exterior d'un subconjunt formen una partició de tot l'espai en tres blocs (o menys quan un o més d'aquests són buits). L'interior i l'exterior són sempre oberts mentre que la frontera és sempre tancada. Els conjunts amb interior buit han sigut anomenats conjunts frontera.^[1]

Si S és un subconjunt de l'espai euclidià, llavors x és un punt interior de S si existeix una bola oberta centrada en x que estigui continguda completament a S.

Aquesta definició es generalitza a qualsevol subconjunt S d'un espai mètric X amb mètrica d: x és un punt interior de S si existeix r > 0 tal que y pertany a S sempre que la distància d(x, y) < r.

Aquesta definició es generalitza a espais topològics canviant «bola oberta» per «conjunt obert». Sigui S un subconjunt d'un espai topològic X. Llavors, x és un punt interior de S si x pertany a un subconjunt obert de S. Equivalentment, x és un punt interior de S si existeix un entorn de x que estigui contingut a S.

L'interior d'un conjunt S és el conjunt de tots els punts interiors de S. L'interior de S s'escriu int(S), Int(S) o S^o. L'interior d'un conjunt té les propietats següents.

• int(S) és un subconjunt obert de S.
• int(S) és la unió de tots els conjunts oberts continguts a S.
• int(S) és el subconjunt obert més gran contingut a S.
• Un conjunt S és obert si i només si S = int(S).
• int(int(S)) = int(S) (idempotència).
• Si S és un subconjunt de T, aleshores int(S) és un subconjunt de int(T).
• Si A és un conjunt obert, aleshores A és subconjunt de S si i només si A és subconjunt de int(S).

De vegades es pren la segona o la tercera propietat de més amunt com a definició de l'interior topològic.

Aquestes propietats també es satisfan si es reemplacen el termes "interior", "subconjunt", "unió", "contingut a", "més gran" i "obert" per "clausura", "superconjunt", "intersecció", "que conté", "més petit" i "tancat", respectivament. Per saber-ne més, vegeu la secció Operador d'interior més avall.

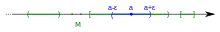
• En qualsevol espai topològic, l'interior del conjunt buit és el conjunt buit.
• En qualsevol espai topològic X, si ${\displaystyle A\subset X}$, int(A) està contingut a A.
• Si X és el conjunt de nombres reals ${\displaystyle \mathbb {R} }$ amb la topologia euclidiana, llavors int([0, 1]) = (0, 1).
• Si X és el conjunt ${\displaystyle \mathbb {R} }$ amb la topologia euclidiana, llavors l'interior del conjunt ${\displaystyle \mathbb {Q} }$ de nombres racionals és buit.
• Si X és el pla complex ${\displaystyle \mathbb {C} =\mathbb {R} ^{2))$, llavors int${\displaystyle (\{z\in \mathbb {C} :|z|\leq 1\})=\{z\in \mathbb {C} :|z|<1\}.}$
• En qualsevol conjunt ${\displaystyle {\mathbb {R} }^{n))$ amb la topolgia euclidiana, l'interior de qualsevol conjunt finit és el conjunt buit. Això no és cert però en altres conjunts amb la topologia euclidiana induïda, per exemple ${\displaystyle \mathbb {N} }$.
• En qualsevol espai amb la topologia en què tots els conjunts són oberts, int(A) = A per tot conjunt A.
• En qualsevol espai amb la topologia en què els únics oberts són el conjunt buit i el propi espai (anomenada topologia grollera), l'interior d'A és el conjunt buit per tot A.

En el conjunt de nombres reals es poden utilitzar topologies diferents a l'estàndard.

• Si ${\displaystyle X=\mathbb {R} }$, on ${\displaystyle \mathbb {R} }$ té la topologia del límit inferior, llavors int([0, 1]) = [0, 1).
• Si es pren a ${\displaystyle \mathbb {R} }$ la topologia en què tots els conjunts són oberts, aleshores int([0, 1]) = [0, 1] (és un cas particular de int(A) = A en topologies on tot conjunt és obert).
• Si es pren a ${\displaystyle \mathbb {R} }$ la topologia en què els únics conjunts oberts són el conjunt buit i el mateix ${\displaystyle \mathbb {R} }$, aleshores int([0, 1]) és el conjunt buit (és un cas particular de l'interior d'A és el conjunt buit per tot A en topologies grolleres).

Aquests exemples mostren que l'interior d'un conjunt depèn de la topologia de l'espai subjacent. Els dos últims exemples són per tipus concrets de topologies.

• En qualsevol espai discret, com que tots els conjunts són oberts, tots els conjunts són iguals al seu interior.
• En qualsevol espai indiscret X, com que els únics conjunts oberts són el conjunt buit i el mateix X, es té que int(X) = X i per qualsevol subconjunt propi A de X, int(A) és el conjunt buit.

L'operador d'interior ^o és dual a l'operador clausura ^—, en el sentit que

S^o = X \ (X \ S)^—,

i també

S^— = X \ (X \ S)^o

on X és l'espai topològic que conté S, i la barra obliqua inversa denota la diferència de conjunts.

Per tant, la teoria abstracta d'operadors de clausura i els axiomes de clausura de Kuratowski es poden traduir fàcilment al llenguatge dels operadors d'interior, canviant els conjunts pels seus complementaris.

L'exterior d'un subconjunt S d'un espai topològic X, escrit ext(S) o Ext(S), és l'interior int(X \ S) del complementari. Alternativament, pot definir-se com a X \ S^—, el complementari de la clausura de S. Moltes propietats es dedueixen directament a partir de les de l'operador d'interior, com les següents.

• ext(S) és un conjunt obert que és disjunt amb S.
• ext(S) és la unió de tots els conjunts oberts que són disjunts amb S.
• ext(S) és el conjunt obert més gran que és disjunt amb S.
• Si S és subconjunt de T, llavors ext(S) és a superconjunt de ext(T).

A diferència de l'operador d'interior, ext no és idempotent, però es compleix que:

• ext(ext(S)) és un superconjunt de int(S).

Dues figures a i b són anomenades d'interior disjunt si la intersecció dels seus interiors és buida, és a dir, si els seus interiors són disjunts. Les figures amb interiors disjunts poden intersecar-se (tenir punts comuns) a la frontera.

• Teorema de la corba de Jordan

• Interior a PlanetMath (anglès)

Viccionari